SUNY Geneseo Department of Mathematics

Introduction to Scalar Line Integrals

Wednesday, November 14

Math 223 01
Fall 2018
Prof. Doug Baldwin

Return to Course Outline

Previous Lecture

Misc

Colloquiua

History of calculus today: 2:30, Newton 202.

Monday November 19, 4:00 PM, Marcus Elia, “NTRU: An Example of a Quantum-Resistant Public Key Cryptosystem.”

Thursday November 29, 2:30, Jessalyn Bolkema, title forthcoming.

Wednesday December 5, speaker and title forthcoming.

Extra credit for the usual write-up on any of these.

Questions?

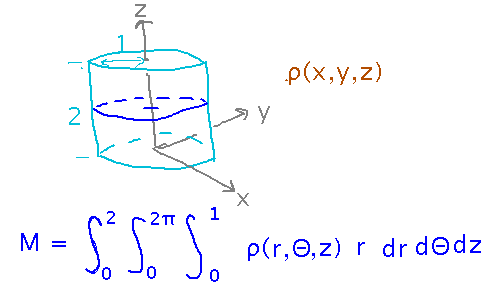
Setting up the bounds for question 3 in the multivariable integrals problem set?

The problem describes a cylinder with variable density, and asks you to find its mass. To get mass from density, you can integrate density over the volume in question (the cylinder). Now think about the bounds, starting with the easy ones: the easiest is probably that z ranges from 0 to 2. Then for each z value in this range, you have to integrate around a circular slice of the cylinder, which suggests polar coordinates -- in polar form, the circles have bounds of 0 to 1 for radius, and 0 to 2π for angle.

Cylinder of radius 1 and height 2 as integral over height, angle, and radius

Line Integrals

Part of section 6.2.

Example

The area of the back wall of the greenhouse we used as an example last Thursday.

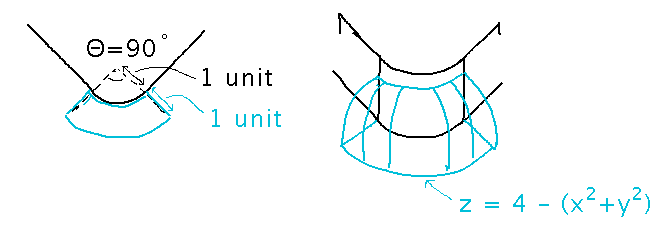
Plan and 3D views of greenhouse with quart-circle wall of height 4 - (x^2+y^2)

What’s going on here: how to conceptualize the solution, and how does it connect to the reading?

Think of this as finding an area (of the wall) under a curve (the one along which the greenhouse roof intersects the wall), which would be a one-dimensional integral. Except the line along which you need to integrate isn’t a nice straight x axis, its a curve in the xy plane.

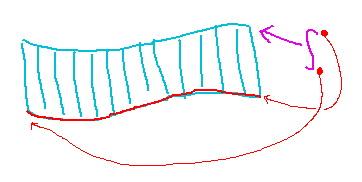
Integrating a curve along a curved path

Such integrals are “line integrals.”

Solve it

The function to integrate is the height-of-the-roof function. Conceptually we need to integrate it along a curve (“C” in typical examples), and we’re integrating with respect to little increments of distance along that curve (“ds”).

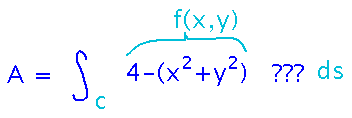
Integral over some curve C of 4 - (x^2+y^2) with respect to arc length

The key idea for capturing the curve is to do so like we did in the past when we wanted to describe curves: as a parameteric (aka vector valued) function.

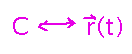
The curve corresponds to a parametric function of t

Then we can substitute the x and y components of r(t) for x and y in the function we’re integrating, and remember that arc length is the integral of the magnitude of r′(t) to get that differential arc length (ds) should be the magnitude of r′(t) dt, to get the second key idea in evaluating arc length integrals:

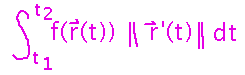
Integral of f(r(t)) times magnitude of r prime

For this particular problem, r(t) has to describe a quarter circle:

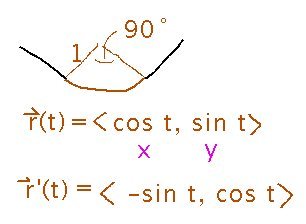
Greenhouse wall forms a quarter circle of radius 1

Now figure out the bounds on t to get the quarter circle (0 to π/2). Then we can finally set up and evaluate the integral:

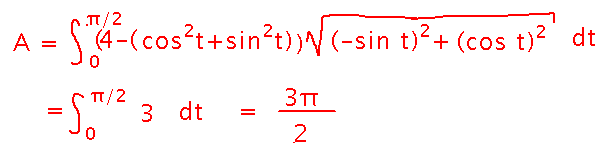
Integrating height in terms of t times magnitude of r prime

Key Points

Line integrals are 1-dimensional integrals along arbitrary paths rather than along an axis.

Describe the path in parametric form.

Equation for evaluating a line integral, given a parametric path.

Problem Set

See handout for details

More examples and practice with scalar line integrals.

Next Lecture