Misc
Grading suggestion: would it help make problem set grading more transparent/objective if each ability I expect you to demonstrate on a problem set (e.g., “abilities” from the latest problem set include “how to evaluate multiple integrals with general bounds,” “how to convert double integrals in rectangular coordinates to polar form,” etc.) were graded with anywhere from 0 to 3 “checkmarks,” where 1 is for showing partial ability, 2 for showing that you completely and consistently display that ability, and the third is for being able to show in your verbal explanation that you really do understand what you did. The grade for the problem set as a whole would be computed by dividing the number of checkmarks you earn by the maximum possible and rounding to the nearest multiple of 1/4, with a rounded value of 4/4 corresponding to a grade of 8, 3/4 to 6, 2/4 to 4, 1/4 to 2, and 0/4 to 0; to that base grade I’d add 1 point if you somehow engaged more deeply with the problem set than you need to in order to solve the problems.
This idea seems interesting enough that we’ll try it on the next problem set (probably handed out Wednesday).
Whatever we do though, grading will never be totally “objective.” There will always be some judgement calls (i.e., “subjectivity”) on such things as how serious a mistake is. Rounding grades to 8, 6, 4, or 2 points is consciously intended to smooth out the effects of these judgement calls. For instance 2 people may make different mistakes involving different judgement calls about their severity, but if the overall effect is that both people showed that they mostly but not entirely get what I’m trying to develop through a problem set, then both get the same grade (say, 6).
To earn 10 points on a problem set, I need to look at it and say “Oh my God, I didn’t know this problem set had such a good solution.” That’s a deliberately high hurdle, but some people do occasionally make it, and it ensures that even people who routinely get 9s have something to try for.
Ways of “engaging more deeply” with a problem set that I’ve recently seen include solving a problem (or problems) in multiple ways, exploring how to apply tools we’re learning about to one or more problems when not asked to (in this course, that often means looking at ways to check solutions with Mathematica), commenting or asking questions during grading that show that you’re thinking about connections between a problem set and other parts of this course or other courses, etc.
Questions?
How to set up the equations for problem 5 on the latest problem set (the volume of the “spherical ring”)?
To understand the problem, imagine boring a hole through a croquet ball, along the z axis. The basic question is “how much wood is left in the ball afterwards?”
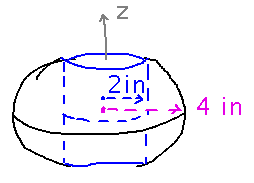
Notice that boring the hole completely removes a little bit of material from the top and bottom of the ball, which keeps you from solving the problem by just subtracting the volume of a cylinder from the volume of a sphere.
Start building an equation by thinking of this in polar form, particularly that you can sweep out points in a plane within the ball by imagining a line rotating through angles between 0 to 2π, and then considering the points on that line between radius 2 (the radius of the cylinder) and the outside of the sphere. This suggests a polar integral of the general form
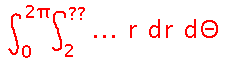
But now the distance to the outside of the sphere depends on z. To see how, use the Pythagorean Theorem. The distance from the z axis to the outside of the sphere, r, is the length of one leg of a right triangle, whose other leg has length z and whose hypotenuse has length 4 (the radius of the sphere).
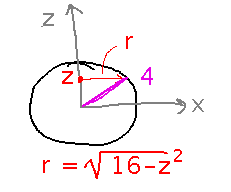
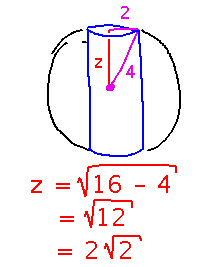
This suggests a third integral, namely over z values. But what are its bounds? Use the Pythagorean Theorem again to find them, this time using a triangle whose hypotenuse runs from the center of the sphere to the top edge of the cylinder (again, the length is the radius of the sphere), and that has one leg whose length is the radius of the cylinder, 2. The other leg is the z coordinate for the top of the bored-out sphere:
So finally we have a complete volume integral (i.e., integral over the region of dV) we can use:
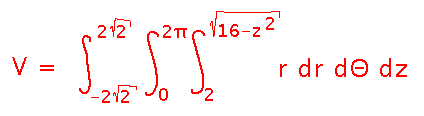
Next
Scalar line integrals.
What is the area of the back wall of the greenhouse from last Thursday’s integration example?
Read “Scalar Line Integrals” in section 6.2.