SUNY Geneseo Department of Mathematics

More Examples of Integration in Polar Coordinates

Thursday, November 8

Math 223 01
Fall 2018
Prof. Doug Baldwin

Return to Course Outline

Previous Lecture

Questions?

Double Integrals in Polar Coordinates

Section 5.3.

First Example

What’s the volume between the circle x2 + y2 = 4 and the surface z = 4 - x2 + y2 ?

Hyperbolic paraboloid 4 - x^2 + y^2 above circle

We figured out what the polar integral looks like, namely

Integral from r=0 to 2 of integral from Theta=0 to 2 pi of r(4-(rcos(Theta))^2+(rsin(Theta))^2)

Now evaluate it. Start by simplifying the integrand a little:

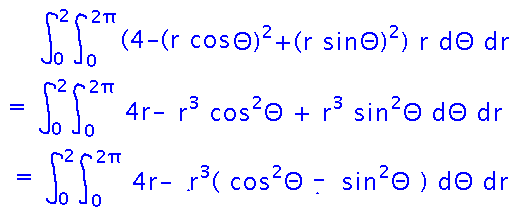
Distribute multiplication by r, expand squares of r times trig functions

But now there’s this “cos2 - sin2” part that looks unfamiliar. This is where remembering trig identities comes in handy, they too are things you can use to simplify expressions. In this case, use the identity that cos2x - sin2x = cos(2x):

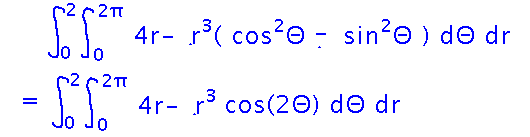
cos^2(Theta) - sin^2(Theta) becomes cos(2Theta)

The rest of the integration is easier, possibly helped along by a u-substitution for integrating cos 2Θ.

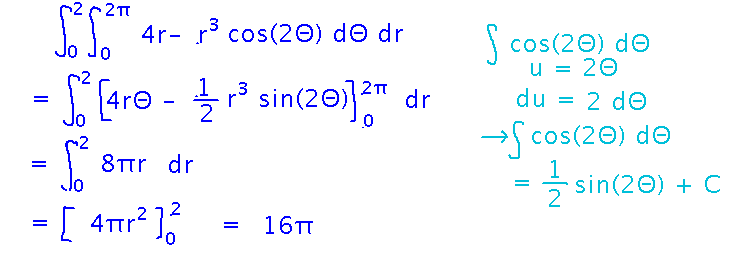
With cos(2Theta) integrating to sin(2Theta)/2, volume is 16 pi

More Interesting Bounds

Imagine a greenhouse attached to a corner of a larger building. The greenhouse is a section of a sphere:

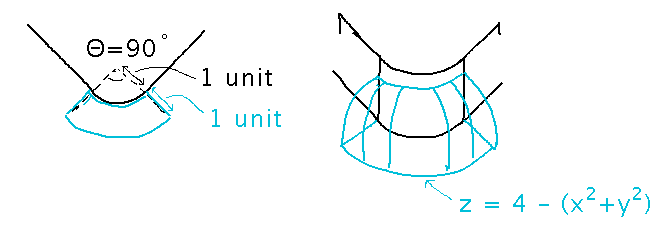
2D and 3D views of greenhouse subtending 90 degree angle and distances from 1 to 2 units from origin

What is the volume enclosed by the greenhouse?

The most challenging part here is setting up the integral. Much as I’ve found bounds for rectangular integrals by thinking of a “slider” that moves through the values of one variable while asking you to think about the values the other(s) take on, thinking about an angle slider (or maybe “dial,” since it turns) that goes over the values of the central angle that cover the greenhouse, while asking what values of r cover the greenhouse as it does so, might help. The angle values end up being anything from 0 to π/2, and r values range from 1 to 2.

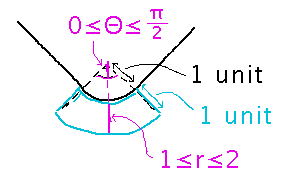
Now we have bounds. To figure out an integrand, recall that x2+y2 = r2, and remember the “r dΘ” term that you need for polar integrals:

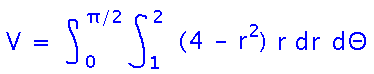
Integral from 0 to pi/2 of integral from 1 to 2 of r times 4 - r^2

Evaluating the rest of the integral just uses standard techniques for integrating polynomials:

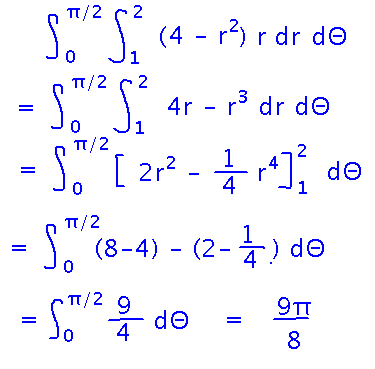
Volume integral evaluates to 9 pi / 8

Key Points

Remember trig identities as tools for algebraic simplification.

Recall how to set up polar integrals: describe the shape you’re integrating over in polar form to get bounds, use rectangular-to-polar equations to convert information given in rectangular form to polar, remember the extra “r” factor in the integrand.

Next

Some physical applications of multiple integrals.

How should you tilt a pyramid to make it balance on its tip?

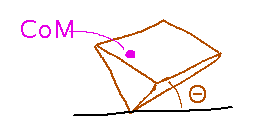
Upside down pyramid tilted to put center of mass over tip

Read section 5.6.

Bring your computer to class for evaluating integrals.

Next Lecture