SUNY Geneseo Department of Mathematics

More about Scalar Line Integrals

Thursday, November 15

Math 223 01
Fall 2018
Prof. Doug Baldwin

Return to Course Outline

Previous Lecture

Misc

Colloquiua

Correction to Monday information (Marcus Elia, public key cryptosystem)

The time is 2:30 - 3:30.

The place is Newton 203.

Questions?

Line Integral Examples

Imagine a dust/gas collector with an opening of 1 cm2. Moving distance ds through material of density ρ(x,y,z) g/cm3 it collects ρ(x,y,z) ds grams of sample.

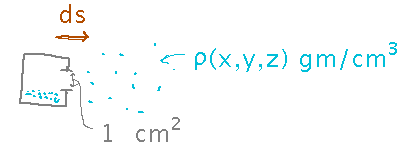
Sampling box moving through dust cloud

Example 1

Suppose this collector moves along the arc r(t) = 〈 cos t, sin t, t 〉from (1,0,0) to (0,1,π/2) in a dust cloud of density ρ(x,y,z) = 1 / (x2+y2+z2).

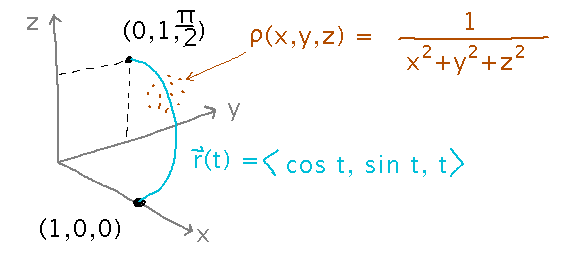
Quarter-helix path from (1,0,0) to (0,1,pi/2)

How much dust does it collect?

The first key idea is that if moving a short straight distance ds collects ρ(x,y,z) ds grams, then the amount collected while moving along a longer curved path is the line integral of ρ(x,y,z) ds along that path (because the total amount collected can be thought of as a sum over lots of tiny straight segments of ρ(x,y,z) ds, i.e., a Riemann sum that becomes the integral as the segments get shorter).

We can evaluate this line integral using the “f of r of t times magnitude of r-prime” formula, and we even have r(t), but need the bounds on t. You can find them by setting the starting and ending points equal to the vector function for r and solving for t:

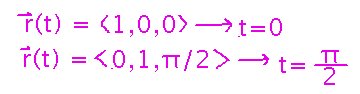
(cos t, sin t, t) equals (1,0,0) if t = 0, and equals (0,1,pi/2) if t = pi/2

Finally, we can set up and evaluate the integral:

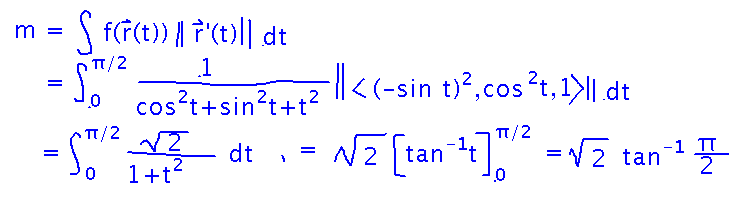
Integrating 1/(cos^2(t)+sin^2(t)+t^2) times magnitude of ((-sin t)^2, cos^2(t), 1)

Example 2

What if the collector moves along 2 straight lines instead: from (1,0,0) to (1,1,1) and then to (0,1,1)?

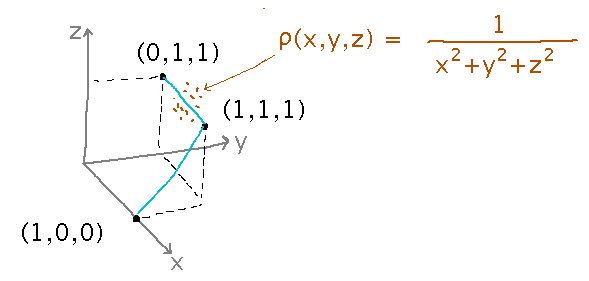
Two straight lines through a dust cloud

One consequence of integrals being derived from sums is that you can split the interval over which you’re evaluating an integral (including line integrals) into sub-intervals and add the integrals over each sub-interval:

Series of rectangles split into 2 consecutive series of rectangles

This is helpful for line integrals over paths that don’t have one parametric form, because you can integrate over each part of the path separately and add the results. Applying this idea to this problem gives two parametric forms for the path (notice that are many possible parametric forms for each part, and it doesn’t matter which you pick, although some may be easier than others to differentiate and integrate):

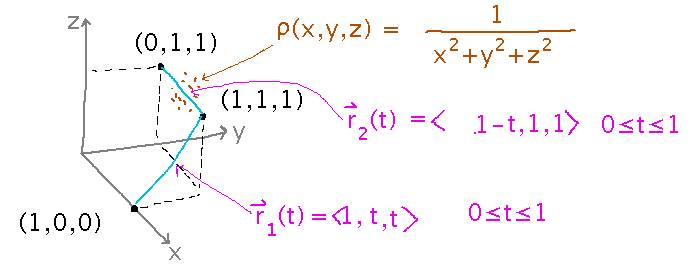
Segments are (1,t,t) and (1-t,1,1)

The total mass collected is now the sum of two integrals:

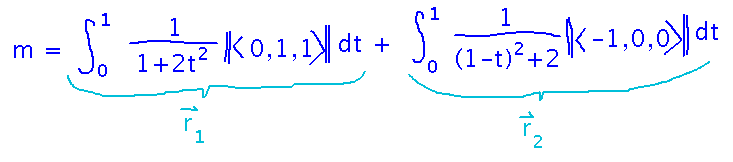
Sum of integrals over path 1 and path 2

These integrate similarly to how the first example did, with the help of a couple of u-substitutions.

Next

The other kind of line integral: line integrals of “vector fields.”

Find out what a vector field is: read...

... in section 6.1.

Next Lecture