Local Extreme Values

Return to Course Outline

Previous Lecture

Misc

Typo

Question 2 in problem set 8 should ask you to find dP/dt.

Hour Exam 2

Next Monday (October 29).

Covers material since exam 1, e.g., arc length and curvature, multivariable functions, limits of multivariable functions, partial derivatives, tangent planes and linearization, the chain rule, gradients, directional derivatives, etc.

Rules and format otherwise similar to exam 1, especially open references and calculators rules.

A collection of practice questions, taken from past exams, is now available in Canvas.

Questions?

Local Extrema

First two subsections of section 4.7.

Example

Where does f(x,y) = 10 - x² - y² + xy + 4x + 2 have its largest value?

Basic idea is that extreme values occur at (x,y) points where both partial derivatives are 0 (or undefined). So start by finding those derivatives:

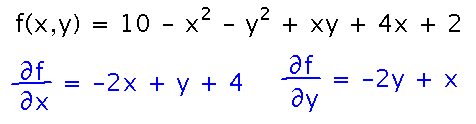
Setting both equal to 0 creates a system of equations to solve:

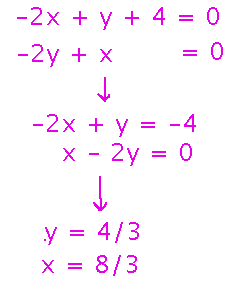
(Plugging these x and y values into f(x,y) gives the actual maximum value of the function.)

How do you know it’s the largest?

Analogous to the second derivative test for single-variable functions, there’s a second-derivative-based test for multivariable functions too. It involves 2 steps, first finding the “discriminant”:

Since the discriminant is greater than 0, we have either a maximum or a minimum. The sign of the second derivative with respect to x twice indicates which: since that derivative is negative, this critical point corresponds to a maximum. (If the second derivative were positive the critical point would be a minimum, and if the discriminant had been negative the critical point would be a saddle point regardless of the second derivative.)

Why does a negative second derivative imply a maximum? Imagine crossing over a maximum in the x direction: as x increases, the 1st derivative is initially positive, then switches to negative as you cross the maximum. So the first derivative must be decreasing, implying a negative second derivative.

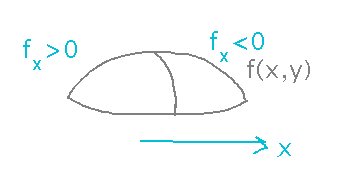
Symmetrical reasoning explains the positive second derivative for a minimum. And you can use similar reasoning to show that you could just as well distinguish minimum from maximum using the second derivative with respect to y twice.

Key Points

Minima and maxima occur where partials both equal 0 or are undefined.

The 2nd derivative test distinguishes maxima from minima from saddle points.

Absolute Extrema

Last subsection of section 4.7.

Example

Find the minimum and maximum values of z = (x-2)² + (y-1)² over the closed triangle with vertices (0,0), (3,0), and (3,3).

Check for minima and maxima of three sorts:

• Ones at critical points, i.e., where the partial derivatives are 0.
• Ones along the edges of the region.
• Ones at the corners of the region.

Key Points

The procedure for finding absolute minima and maxima.

Next

Carry out the above procedure for the given example.

Next Lecture