More about Directional Derivatives

Return to Course Outline

Previous Lecture

Misc

Hour Exam 2

Next Monday (October 29).

Covers material since exam 1, e.g., arc length and curvature, multivariable functions, limits of multivariable functions, partial derivatives, tangent planes and linearization, the chain rule, gradients, directional derivatives, etc.

Rules and format otherwise similar to exam 1, especially open references and calculators rules.

I will find a practice exam.

Questions?

Directional Derivatives

Auditorium Example

From last time, we had...

• An equation for the ceiling, z(x,y) = √(400-4y²)
• A gradient vector, ∇z = 〈 0, -4y / √(400-4y²) 〉

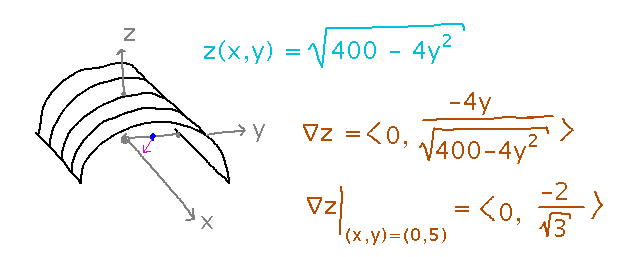
If you are at (0,5) (where ∇z = 〈 0, -2/√3 〉) and walk in the direction that makes the distance between you and the ceiling increase fastest, how fast is that distance changing? The gradient gives the direction of largest (and so most positive) rate of change, and it’s magnitude is that rate of change.

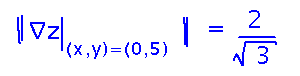
Because you’re walking parallel to one of the axes, you could also solve this particular example by finding the derivative of z with respect to y (the axis you’re walking parallel to). But since that derivative is the rate of change per unit increase in y, and you’re walking in the decreasing y direction, multiply by -1.

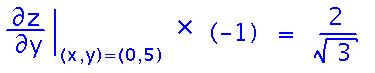
Now suppose you walk in direction 〈 1, -1 〉from (0,5). How fast does the distance from your head to the ceiling change?

Now you need a directional derivative, D_u(0,5) where u is a unit vector in the direction you’re walking,〈 1, -1 〉.

What’s going on with u = 〈 cos Θ, sin Θ 〉? Those are the components of a unit vector at angle Θ to the x axis, from the definitions of sine and cosine.

Find the unit direction vector u by dividing the non-unit direction vector d by its magnitude:

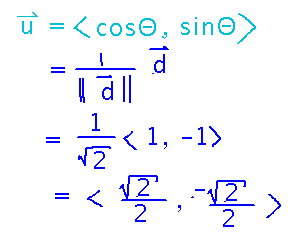
And finally there are several ways to calculate the directional derivative, the easiest in my mind being as the dot product of the gradient and the unit direction vector:

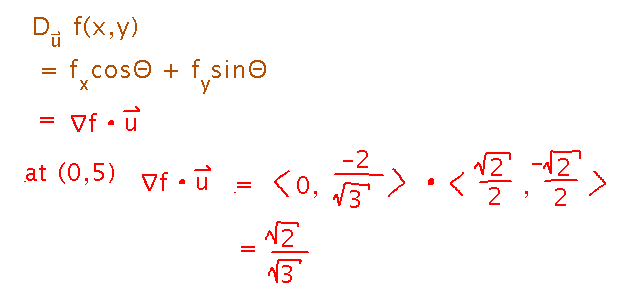
Key Points

The directional derivative is the rate at which f changes per unit change in (x,y) in a given direction.

Calculated as the dot product of the gradient with a unit direction vector.

Which leads to the fact that the maximum directional derivative is the magnitude of the gradient, and occurs when you move in the gradient direction.

Problem Set

See handout for details.

Next

Local minima and maxima.

Guiding example: Where does the function f(x,y) = 10 - x² - y² + xy + 4x + 2 have its largest value?

Read these subsections of section 4.7:

• Critical Points
• Second Derivative Test

Next Lecture