Absolute Extreme Values

Return to Course Outline

Previous Lecture

Misc

Hour Exam 2

Next Monday (October 29).

Covers material since exam 1, e.g., arc length and curvature, multivariable functions, limits of multivariable functions, partial derivatives, tangent planes and linearization, the chain rule, gradients, directional derivatives, etc.

Rules and format otherwise similar to exam 1, especially open references and calculators rules.

A collection of practice questions, taken from past exams, is now available in Canvas.

Questions?

Absolute Maxima and Minima

Find the minimum and maximum values of z = (x-2)² + (y-1)² over the closed triangle with vertices (0,0), (3,0), and (3,3).

Process

1. Find critical points (derivatives equal 0)
2. Check edges (typically a single variable maximum/minimum)
3. Check corners

Carry that out for this example:

Key Points

The procedure for finding them.

Next

Optimization problems.

Guiding example: Remember Geneseo Widget Works producing am/10 - m widgets per hour with a assemblers and m managers. If assemblers earn $15/ hour and managers earn $25/hour, and GWW can afford to pay $1000/hour in salaries, what’s the optimal number of assemblers and managers?

Roughly speaking, this requires solving a local extreme value problem while observing certain constraints on the values of variables:

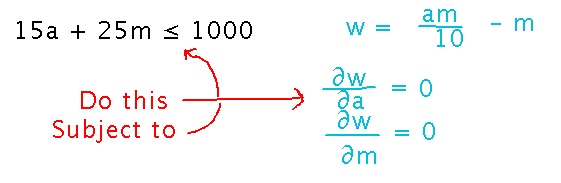
Read section 4.8 to see one way of doing it for multivariable functions.

Next Lecture