SUNY Geneseo Department of Mathematics

More Induction

Friday, March 9

Math 239 01
Spring 2018
Prof. Doug Baldwin

Return to Course Outline

Previous Lecture

Questions?

Proof by Induction

Formal Presentation

See how I formally wrote the proof about the sum of the first n natural numbers from Wednesday’s class.

Another Sum

Prove that 2¹ + 2² + ... + 2ⁿ = 2ⁿ⁺¹ - 2.

Theorem: For all natural numbers n, 2¹ + 2² + ... + 2ⁿ = 2ⁿ⁺¹ - 2 (Eq. 1).

Proof: We will use induction on n to prove that for all natural numbers n,

For the base case, we note that

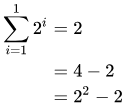
Sum from 1 to 1 of 2^i = 2 = 2^2 - 2

For the induction step, we assume that k is a natural number such that

(Eq. 2)

and will show that

Adding 2^k+1 to both sides of Eq. 2 yields

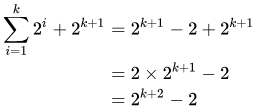
Sum from 1 to k of 2^i + 2^(k+1) = 2^(k+1)-2+2^(k+1) = 2^(k+2)-2

Finally, noting that

completes the induction step.

Since we have now shown that Eq. 1 holds for n = 1, and that when it holds for n = k it also holds for n = k+1, it follows by the principle of mathematical induction that Eq. 1 holds for all natural numbers. We have thus shown that for all natural numbers n, 2¹ + 2² + ... + 2ⁿ = 2ⁿ⁺¹ - 2. QED.

A Non-Sum Example

Theorem 3.28, part 3: for all integers a and b, and all natural numbers n and m, if a ≡ b (mod n), then a^m ≡ b^m (mod n).

Proof: We will use induction on m to prove that for all integers a and b, and all natural numbers n and m, if a ≡ b (mod n), then a^m ≡ b^m (mod n).

For the base case, note that a¹ = a, b¹ = b, and a ≡ b (mod n), so a¹ ≡ b¹ (mod n).

For the induction step, assume that k is a natural number such that a^k ≡ b^k (mod n). We then show that a^k+1 ≡ b^k+1 (mod n). Notice that a^k+1 = a a^k, b^k+1 =b b^k, and that a ≡ b (mod n) and a^k ≡ b^k (mod n). Therefore by Theorem 3.28 part 2, a^k+1 ≡ b^k+1 (mod n).

We have now shown that a¹ ≡ b¹ (mod n) and that for any natural number k, if a^k ≡ b^k (mod n) then a^k+1 ≡ b^k+1 (mod n). It therefore follows by the principle of mathematical induction that for all integers a and b, and all natural numbers n and m, if a ≡ b (mod n), then a^m ≡ b^m (mod n). QED.

Key Points

Induction proofs extend the “template” structure for a formal proof:

Say at the beginning that you’re using proof by induction, and what variable you’ll do induction on.
The body of the proof has two distinct parts, the base case and the induction step; be sure both are clearly identified.
The induction part should start with a statement of the induction hypothesis (i.e., that the theorem is true of some natural number k) and what you will prove from it (i.e., that the theorem is true of k+1).

Look for a way to use the induction hypothesis early in the induction step.

Extensions to the basic principle of mathematical induction.

Read section 4.2.

Next Lecture