Misc: GROW STEM Events
Title IX Workshop
Today, 4:00 - 5:00 PM, Newton 204
By Tamara Kenney, Geneseo Title IX coordinator
Club Interest Meeting
Tomorrow (Thursday, March 8), 5:00 PM, Newton 204
Part of creating a student organization focused on diversity in STEM fields.
Questions?
Induction
Section 4.1.
Inductive Sets
Is the set of prime numbers, i.e., { 2, 3, 5, 7, 11, 13, 17, ... }, inductive? No, because it fails the “k+1” test, i.e., there are members, k, whose successors, k+1, are not in the set, for example 5 is in the set but 6 is not.
Is the set of integers n such that 2n > 10, i.e., { n ∈ ℤ | 2n > 10 }, inductive? Yes, it’s a set of integers and 2k > 10 implies 2(k+1) > 10 so whenever a value k is in this set so is k+1.
Is { 1/2, 3/2, 5/2, 7/2, ... } inductive? No, it’s not a subset of the integers.
A Bridge to Proof by Induction
Prove that S = {n ∈ ℕ | 3n is odd} is in fact equal to ℕ.
Axiom: If T is a subset of ℕ, and 1 ∈ T,and T is inductive, then T = ℕ.
So if we can show that 1 is in S and that S is inductive, then S = ℕ.
Proof outline:
31 is odd, so 1 is in S.
If 3k is odd, then 3k+1 is odd. Assume 3k is odd, and show that 3k+1 is also odd. 3k+1 = 3 × 3k, which is an odd number times an odd number, which we know is odd.
Proof by Induction
Proof by induction is essentially what we did with the “bridge” above, except formalized a little more as proving that some claim is true of all natural numbers by showing that the truth set of the claim equals the whole set of naturals.
Example
Complete Progress Check 4.3, proving that 1 + 2 + 3 + ... + n = n(n+1)/2.
Theorem: For all natural numbers, n,
![]() (Eq. 1)
(Eq. 1)
Proof: We prove by induction on n that Eq. 1 holds for all natural numbers n.
For the base case, note that
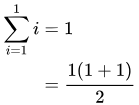
For the induction step, we assume that for some natural number k,
![]()
and will show that
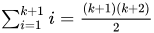
Separating the last term out of the sum on the left side of this equation and then applying the induction hypothesis yields
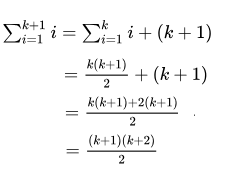
We have thus established that Eq. 1 holds when n = 1, and that for all natural numbers k, if it holds for n = k, it also holds for n = k+1. Thus, by the principle of mathematical induction, we have shown that Eq. 1 holds for all natural numbers n. QED.
Key Points
An inductive set is a set of integers such that if k is in the set, k+1 also is.
Using induction to prove claims about all natural numbers.
Next
More examples of proof by induction.