Introduction to Induction

Misc: GROW STEM Events

Title IX Workshop

Today, 4:00 - 5:00 PM, Newton 204

By Tamara Kenney, Geneseo Title IX coordinator

Club Interest Meeting

Tomorrow (Thursday, March 8), 5:00 PM, Newton 204

Part of creating a student organization focused on diversity in STEM fields.

Questions?

Induction

Section 4.1.

Inductive Sets

Is the set of prime numbers, i.e., { 2, 3, 5, 7, 11, 13, 17, ... }, inductive? No, because it fails the “k+1” test, i.e., there are members, k, whose successors, k+1, are not in the set, for example 5 is in the set but 6 is not.

Is the set of integers n such that 2n > 10, i.e., { n ∈ ℤ | 2n > 10 }, inductive? Yes, it’s a set of integers and 2k > 10 implies 2(k+1) > 10 so whenever a value k is in this set so is k+1.

Is { 1/2, 3/2, 5/2, 7/2, ... } inductive? No, it’s not a subset of the integers.

A Bridge to Proof by Induction

Prove that S = {n ∈ ℕ | 3ⁿ is odd} is in fact equal to ℕ.

Axiom: If T is a subset of ℕ, and 1 ∈ T,and T is inductive, then T = ℕ.

So if we can show that 1 is in S and that S is inductive, then S = ℕ.

Proof outline:

3¹ is odd, so 1 is in S.

If 3^k is odd, then 3^k+1 is odd. Assume 3^k is odd, and show that 3^k+1 is also odd. 3^k+1 = 3 × 3^k, which is an odd number times an odd number, which we know is odd.

Proof by Induction

Proof by induction is essentially what we did with the “bridge” above, except formalized a little more as proving that some claim is true of all natural numbers by showing that the truth set of the claim equals the whole set of naturals.

Example

Complete Progress Check 4.3, proving that 1 + 2 + 3 + ... + n = n(n+1)/2.

Theorem: For all natural numbers, n,

(Eq. 1)

Proof: We prove by induction on n that Eq. 1 holds for all natural numbers n.

For the base case, note that

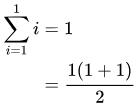
For the induction step, we assume that for some natural number k,

and will show that

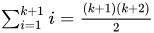
Separating the last term out of the sum on the left side of this equation and then applying the induction hypothesis yields

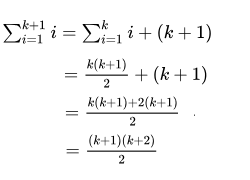
We have thus established that Eq. 1 holds when n = 1, and that for all natural numbers k, if it holds for n = k, it also holds for n = k+1. Thus, by the principle of mathematical induction, we have shown that Eq. 1 holds for all natural numbers n. QED.

Key Points

An inductive set is a set of integers such that if k is in the set, k+1 also is.

Using induction to prove claims about all natural numbers.

Next

More examples of proof by induction.