SUNY Geneseo Department of Mathematics

Variations on Induction

Monday, March 19

Math 239 01
Spring 2018
Prof. Doug Baldwin

Return to Course Outline

Previous Lecture

Misc

Colloquium

Colloquium on inverse problems rescheduled for this Thursday:

Sedar Ngoma, “An Overview of Inverse Problems.”

Thursday, March 22, 2:30 PM, Newton 203.

Extra credit as usual for 1-paragraph connections or other reactions.

Mid-Semester Feedback

A relatively informal anonymous survey on how this course is working for you. Fill it out to whatever extent you want; return by Wednesday.

Questions?

Irrational Numbers?

What is the general form of an irrational number to use in proofs involving irrationals?

There isn’t one, irrationals are simply defined as numbers that aren’t rational, so the best you can say about an irrational number is that it’s not of the form a/b for any integers a and b (with b ≠ 0).

Induction Variations

Section 4.2.

Problem set: see handout for details.

Example: The Extended Principle of Mathematical Induction

A more interesting theorem about sums of powers of 2: for all integers n ≥ 0,

Sum from 0 to n of 2^i = 2^(n+1)-1 (Eq. 1)

To prove this, should the base case be 1 or 0? 0 is the smallest value of n for which the theorem can hold, and there’s actually no reason why you can’t start induction with any integer.

Proof: We will prove by induction on n that Eq. 1 holds for all integers n ≥ 0.

For the base case we consider n = 0, and observe that

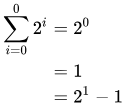
Sum from 0 to 0 of 2^i = 1 = 2^1 - 1

For the induction step, we assume that Eq. 1 holds when n = k, for some integer k ≥ 0, and show that Eq. 1 also holds when n = k+1. To see this, split Sum from 0 to k+1 of 2^i into its first k terms and its (k+1)th term, and simplify:

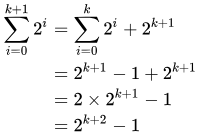
Sum from 0 to k+1 of 2^i = sum from 0 to k of 2^i + 2^(k+1) = 2^(k+1)-1+2^(k+1) = 2^(k+2)-1

Having established a base case of n = 0 and and induction step, we conclude that Eq. 1 holds for all integers n ≥ 0. QED.

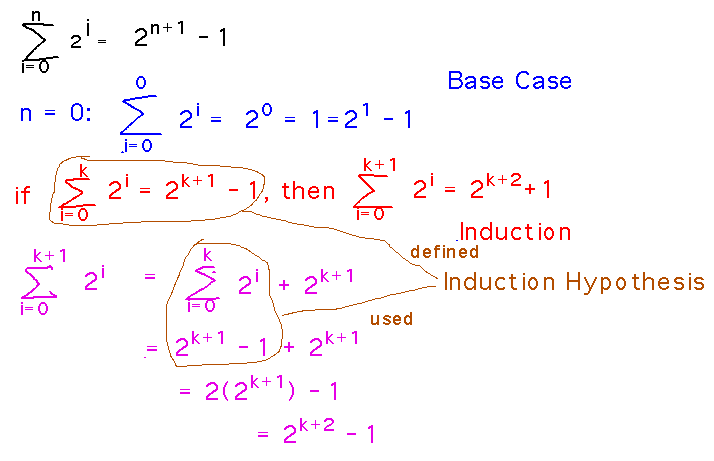
Here’s a more visual version of the proof idea, showing the distinct base case and induction step, and how the induction hypothesis gets used in proving the induction step:

Induction proof consists of base case and induction, which proves an conditional that establishes an induction hypothesis

Example: The 2nd Principle of Mathematical Induction

Progress Check 4.10 / proposition 4.11: for all natural numbers n ≥ 8, there exist non-negative integers x and y such that n = 3x + 5y.

It seems like we could do a proof by induction on n.

Looking at some examples suggests that the proposition is true:

Further examples beyond these suggest that the pattern in the multiples of 5 shown here cycles every 3 values of n.

This will probably use the second principle of induction.

The induction could be something like this: if 8, 9, 10, ... k can be expresed as 3x + 5y, then k+1 can too. The key to moving forward from here is to notice that k+1 = (k-2) + 3.

See what you can do with, or what questions you can come up with about, these ideas by Wednesday.

Meanwhile, here’s a sketch of a proof by weak induction (the first principle) for the proposition without the requirement that x and y be non-negative. The induction is on n:

For the base case, note that 8 = 3×1 + 5×1.

For the induction step, assume k is an integer greater than or equal to 8 such that k = 3x + 5y for integers x and y, and show that k+1 = 3w + 5z for integers w and z. To show this, notice that 1 = 3×2 + 5×(-1) and so

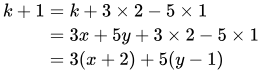
k+1 = 3x + 5y + (3)(2) + (5)(-1) = 3(x+2) + 5(y-1)

Key Points

Induction can start at any integer (the extended principle of mathematical induction).

Strong induction can assume more than just P(k) (the 2nd principle of mathematical induction).

Next

More practice with induction, particularly strong induction.

Next Lecture