Misc
More end-of-semester reminders.
Grade-Related Deadlines
The deadline for withdrawal from classes is the Wednesday, May 6.
The deadline for committing to P/F vs regular grading is May 31. Talk to your advisor about P/F vs regular grading, there are lots of implications for GPA, how graduate schools will look at it, etc.
SOFIs
3 of you have done them as of this morning — thank you! But it would be nice to have more, too.
Questions?
What does the “Extending the Fundamental Theorem of Calculus” section in the reading have to do with anything? It’s one way of understanding Green’s Theorem, i.e., while the fundamental theorems for integration that we’ve seen so far give you a simple way to evaluate an integral over a 1-dimensional region, Green’s Theorem gives you a simple way to evaluate an integral over a 2-dimensional region.
Potential Functions
Before we get to Green’s Theorem, we were going to look at an example where finding a potential function takes a couple of integration and differentiation steps.
Find a potential function for F(x,y,z) = 〈 1/z - ln y, 1/z + ez - x/y, -(x+y)/z2 + yez 〉.
Since F is the gradient of its potential function (f), F’s first component is the derivative of f with respect to x. So integrating that component with respect to x should give us the potential function:

It does, but where single-variable integration would produce a constant of integration, indefinite integration for multivariable functions produces what might be called a “function of integration,” i.e, a term that depends on the variables other than the one you integrated with respect to. Here we called it g(y,z). We need to figure out what this function is.
To do that, realize that the derivative of f with respect to y is the second component of F. So calculate that derivative for f as far as we know it. That will hopefully reveal something about g:

Now we know a derivative of g, so integrate again. Plug the resulting function back into the definition of f, to get a more complete definition:

Once again there’s a function of integration, h(z). One more round of differentiating f (this time with respect to z) and comparing to a component of F reveals that this function is 0, so we have the final version of f:
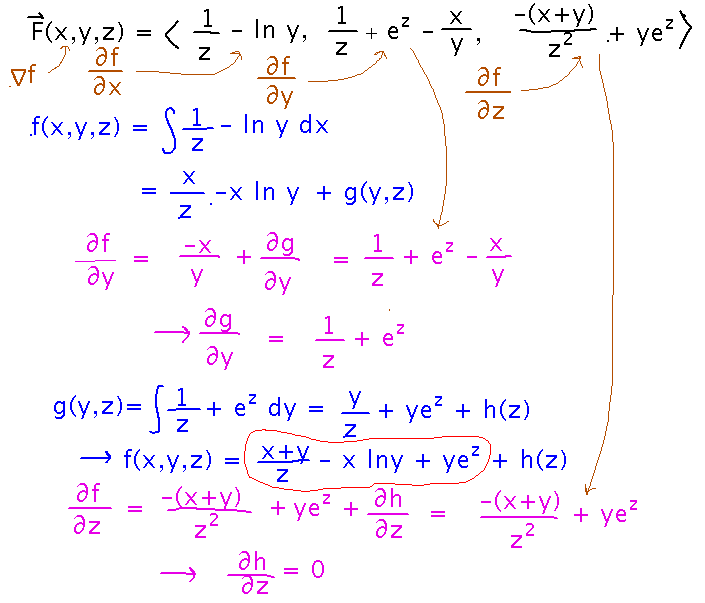
Green’s Theorem
Section 15.4 in the book, particularly “Circulation Form of Green’s Theorem.”
Key Ideas or Questions
Relates a line integral in 2 dimensions around a closed path to a double integral over the area inside that path. Specifically...
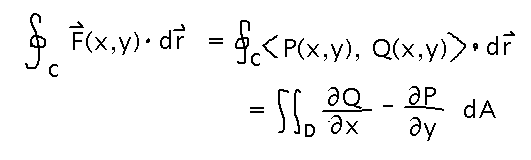
The Last Problem Set
On conservative vector fields and Green’s Theorem.
See the handout for details.
Next
Finish Green’s Theorem.
Please read “Flux Form of Green’s Theorem” (but we probably won’t have time to look at source-free fields and stream functions, so you can stop when you come to them).