SUNY Geneseo Department of Mathematics

More about Green’s Theorem

Wednesday, May 6

Math 223 01
Spring 2020
Prof. Doug Baldwin

Return to Course Outline

Previous Lecture

Questions?

Green’s Theorem

Section 15.4 in our textbook.

Circulation Example

Based on Example 15.4.2.

Use Green’s Theorem to evaluate the integral counterclockwise around a triangle with vertices (-1,1), (3,1), and (3,6) of sin(x²) dx + (4x - y) dy.

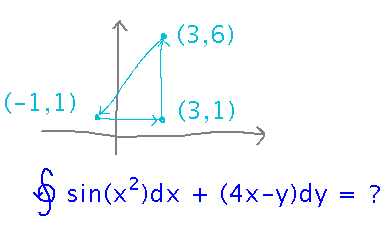
Triangle and line integral around it

Start by identifying P and Q functions and their derivatives:

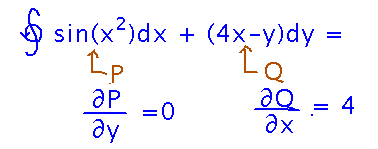
P is function integrated 'd x', Q is integrated 'd y'

Then plug the derivatives into the formula provided by Green’s Theorem:

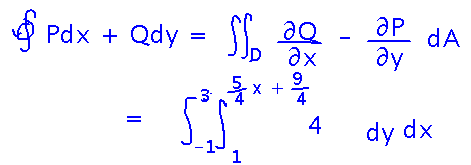
Integrate derivative of Q with respect to x minus derivative of P with respect to y

But before getting too far into the integral, notice that it’s basically an area integral, and so can be evaluated just by finding the area enclosed in the triangular path. This is a good example of how Green’s Theorem can pay off by turning an awkward line integral into a very simple calculation that doesn’t necessarily even require explicitly evaluating an integral.

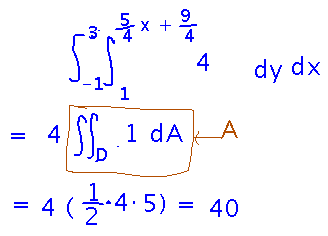
Integral is just 4 times area of the triangle

Question: Why does Green’s Theorem require paths to be traced counterclockwise? I think it’s a more or less arbitrary decision to accommodate the fact that vector line integrals depend, thanks to the dot product in them, on the direction they follow the path. There’s no similar dot product in a double integral over an area, so the proof of Green’s Theorem has to build some assumption about direction into the formula it derives. It could probably just as well have derived a slightly different formula (specifically the negative of the one it uses) by assuming the path was traced clockwise.

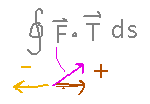
F dot T in integral can be either positive or negative depending on angle between F and T

Flux Example

Green’s Theorem has a second form, which applies to flux integrals:

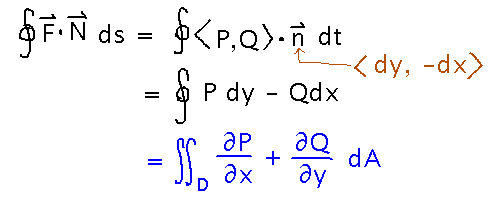
Integral of F dot N equals double integral of derivative of P with respect to x plus derivative of Q with respect to y

For example, find the flux of F(x,y) = 〈 xy, x 〉 across the rectangle with vertices (0,0), (1,0), (1,2), and (0,2) traversed counterclockwise.

Rectangle and flux integral across it

As with the circulation example, start by identifying the component functions and their derivatives:

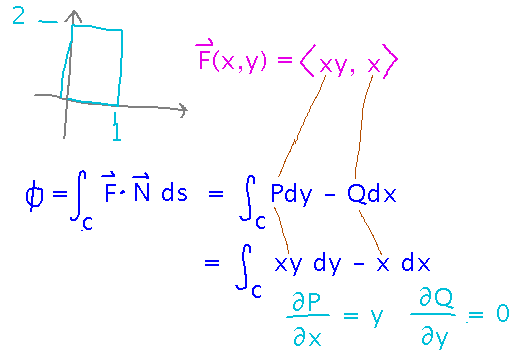
P equals x times y, Q equals x; needed derivatives are y and 0

Then plug the derivatives into the formula from the theorem and integrate:

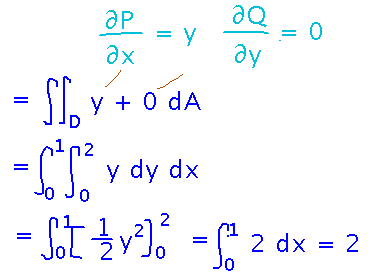
Integrating y over rectangle

No more class meetings.

The last problem set needs to be graded by next Thursday (May 14).

I’m available via email, Google hangout, etc. through the end of finals.

Thank you for taking this course.

(No Next Lecture)