Line Integrals and Conservative Vector Fields

Misc

Thanks to 3 of you have done SOFIs. But more would be even better....

Questions?

Line Integrals and Conservative Vector Fields

Section 15.3

Key Ideas or Questions

The fundamental theorem of line integrals: the integral of ∇f along path r(t) from t=a to t=b is f(r(b)) - f(r(a))

Consequences:

• Any line integral of a conservative field over a closed loop is 0.
• Line integrals of conservative fields are “path independent,” i.e., their values don’t depend on the shape of the curve you integrate along, only on its endpoints.

Finding potential functions is valuable.

Fundamental Theorem of Line Integrals

Give F(x,y,z) = 〈 2 sinx cosx, -sinx siny, 2 cosz sinz 〉= ∇f where f(x,y,z) = sin²x + sinx cosy - cos²z, find the integral of F(x,y,z) along r(t) for 0 ≤ t ≤ π/2, where r(t) = ⟨ t, t², t ⟩.

Use the fundamental theorem of line integrals: evaluate f(r(π/2)) and f(r(0)) and subtract.

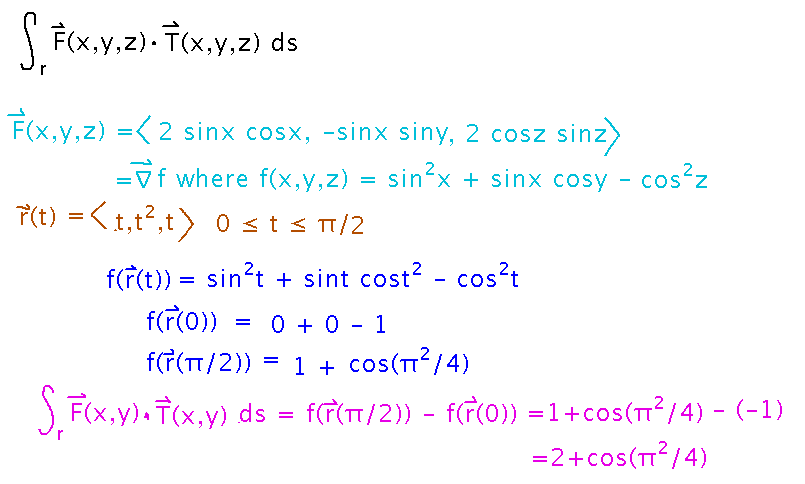
Potential Functions

Find a potential function for F(x,y) = ⟨ e^x cos(e^x), -e^y sin(e^y) ⟩.

Consider finding antiderivatives of both component functions. If they come out the same then that must be the potential function. Try this idea:

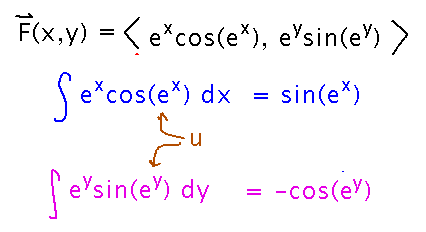
These don’t look the same. But on the other hand we left out the “constants” of integration, which in the case of integrating what are nominally multivariable functions are really functions of the other variable(s). Including them gives us a way to reconcile the two antiderivatives into a single potential function:

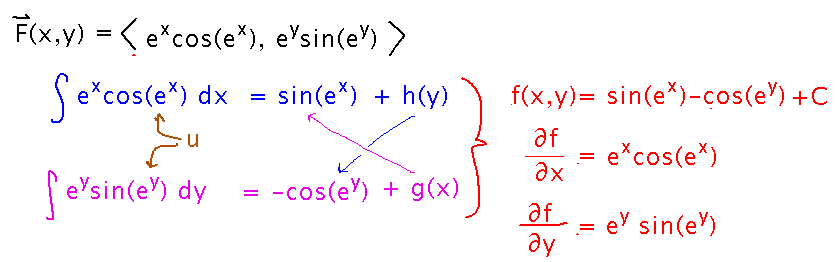
This example was a bit simple, in that each component of F involved just one variable, so they could be integrated independently and then reconciled at the end. A slightly more sophisticated process integrates one component after another, checking each against the appropriate derivative of the potential function as known so far before each integration.

Next

An even more complicated example of finding a potential function.

Then Green’s Theorem.

Please read “Extending the Fundamental Theorem of Calculus” and “Circulation Form of Green’s Theorem” in section 15.4.