SUNY Geneseo Department of Mathematics
Monday, April 13
Math 223 01
Spring 2020
Prof. Doug Baldwin
RIT is hosting a virtual colloquium on “The Evolution of Matlab.”
This Wednesday (April 15), from 1:00 to 1:50.
Contact ndcsma@rit.edu to get the Zoom link.
See https://www.rit.edu/events/sms-colloquium-moler for more information.
I will give a little bit of extra credit if you attend this colloquium and write a paragraph or a few sentences about connections you make to it or other reflections you have on it.
What is the due date for extra credit math videos? May 8, the original final exam date. But let me know if you need an extension.
Multivariable Integration
Today we are (hopefully) finishing what I want to cover from sections 14.2, 14.3, and 14.5 of the textbook.
Integrate f(x,y,z) = xy + yz over the volume between the planes x = 0, y = 0, z = 0 and x + y + z = 1.
The hardest part of this is figuring out what the bounds of the integrals should be. One way to do that is to think about what those bounds mean geometrically: they describe the values over which a variable ranges, so you could, for example, decide to let x range from 0 to 1 (the maximum value it can take on), then for each x value y can range from 0 up to the intersection of the x+y+z = 1 plane with the z = 0 plane (i.e., the line x+y = 1), and finally for each (x,y) pair, z then ranges from 0 to the x+y+z = 1 plane itself:
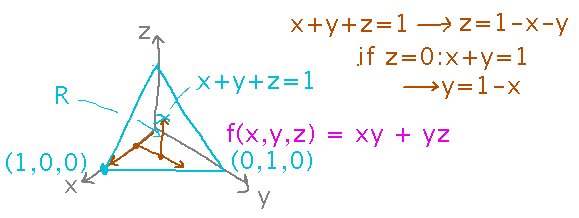
This thinking gives formulas for bounds on the iterated integrals, e.g., for x they are 0 and 1, then y ranging from 0 to the x+y = 1 line implies the upper bound on y is 1-x, and z ranging from 0 to the plane implies the upper bound on z is 1-x-y. Once these bounds are decided, the rest of the integration is mechanical (and tedious):
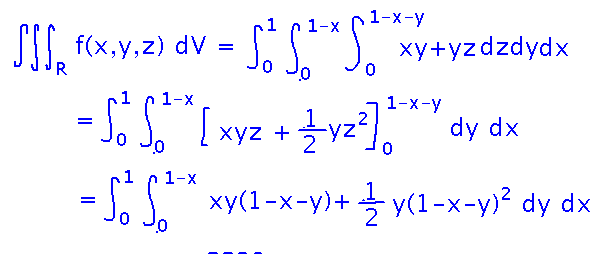
And because the integral is tedious, a good alternative is...
The Integrate command is still the key function to do it.
You can provide intervals to integrate over for multiple variables. The bounds on those intervals can be expressions involving earlier variables.
For example, this notebook illustrates how Mathematica can evaluate the integral above, plus some others we did in class last week.
On multivariable integration.
See the handout for details.
This is another individually graded problem set. Grading is Thursday April 23 through Monday April 27.
Notice that we’ve avoided integrals over circular regions. That’s because such integrals are much easier to do in polar coordinates than in rectangular.
So we’ll look at how that works.
Please read section 14.4 in the textbook.