Integrals over General Regions, Part 2

Return to Course Outline

Previous Lecture

Questions?

Integration over General Regions

Section 14.3 in the textbook.

Two Variables

Integrate 3x - x³y over the region 1 ≤ y ≤ 2 and 0 ≤ x ≤ √y.

This example mainly demonstrates how you can use constant bounds in the y dimension and functions of y as one or both bounds in the x dimension. The outer integral needs to be with respect to y and the inner with respect to x, but otherwise the process is the same as what we’ve been doing:

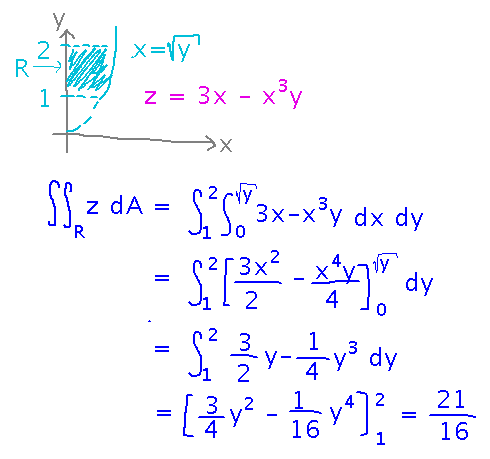
An Application in 3 Variables

Find the volume inside the “bowl” defined by x² + y² ≤ z ≤ 2 and above the rectangle -1 ≤ x ≤ 1, -1 ≤ y ≤ 1.

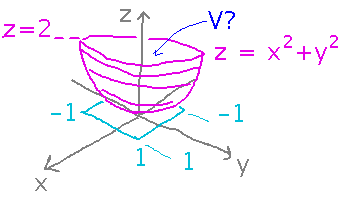
You can set this up as a 3-dimensional integral of 1, generalizing from the formula for area in 2 dimensions. The inner-most integral, over z, has x² + y² as its lower bound, since that’s the z coordinate for the bottom of the bowl. The integration proceeds similarly to how integrals over general regions in 2 dimensions did:

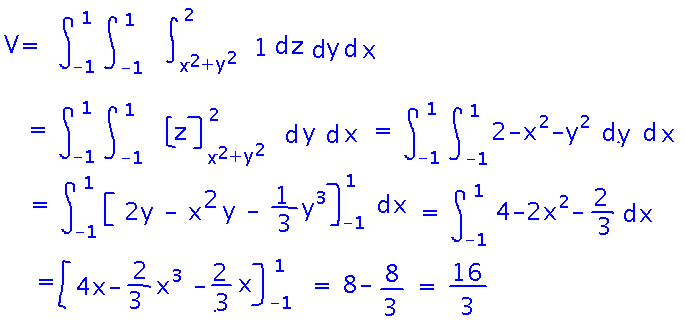
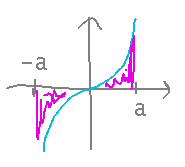
In the last couple of steps here we used the trick that the integral of an odd function (one where f(-x) = -f(x)) over an interval from x = -a to x = +a is always twice the value of the integral from 0 to a.

The main morals here are

• The ideas for integrals over non-rectangular regions extend to more than 2 dimensions
• Such integrals have applications, e.g., finding volumes.

Three Variables

Integrating over general regions in 3 (or more) dimensions can require more thought than doing it in 2 dimensions. Here’s an example that I mostly want to work on Monday, but start thinking about it over the weekend:

Integrate f(x,y,z) = xy + yz over the volume between the planes x = 0, y = 0, z = 0 and x + y + z = 1.

Next

Finish multiple integrals over general regions, especially in more than 2 dimensions.

No new reading.

Next Lecture