Misc
GREAT “Day”: Originally scheduled for next Wednesday, April 22. Now moved to a virtual format that opens on the 22nd and continues through September 30.
Virtual GREAT Day consists of online posters, papers, videos, etc.
See https://www.geneseo.edu/great_day to access exhibits on or after April 22. (But exhibitors who get the most clicks between 9:00 AM and 6:00 PM on the 22nd can win prizes.)
I’ll give the usual extra credit for any one math-related exhibit you write a short description of and reaction to. Description and reaction really can be just 1 or 2 sentences each.
Since this semester’s calendar was built on the assumption that there would be no classes on the 22nd, we won’t meet that day.
Questions?
Integration in Polar Coordinates
Section 14.4 in the textbook.
Key Idea(s) or Questions
You can integrate over r and Θ in polar coordinates, but “dA” aka “dx dy” becomes “r dr dΘ.”
Main Idea
Integrate f(x,y) = x + y2 over the circle x2 + y2 = 1.
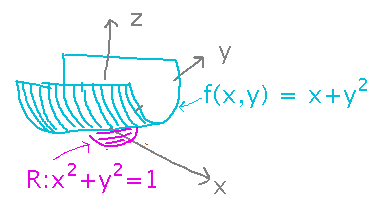
Start by realizing that the circle is just the region 0 ≤ Θ ≤ 2π, 0 ≤ r ≤ 1 in the polar coordinate system. Then use the conversions x = r cosΘ and y = r sinΘ to express f(x,y) as a function of r and Θ. Finally remember that the differential area in the integral is r dr dΘ:
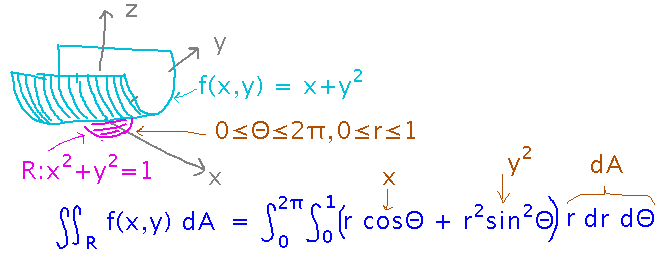
From here, evaluating the integrals is tedious but fairly mechanical. It might help, however, to keep in mind the trigonometric identity sin2Θ = (1-cos(2Θ))/2.
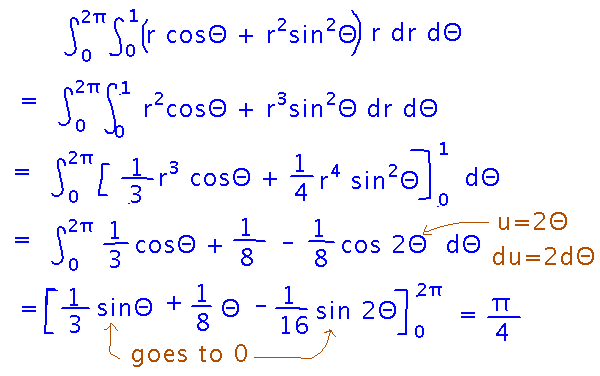
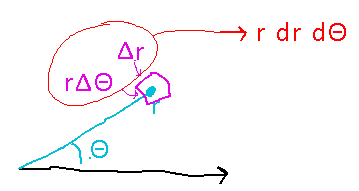
Why is there an r in the dA term?
Polar integrals are still Riemann sums of volumes, i.e., they conceptually multiply an infinitesimally small area by the height of a function above that area. The area is measured on two sides by small changes in r, i.e., distance, which is good because you need to multiply two distances to get an area. But on the other sides the area is measured by small changes in Θ, i.e., angle, which is not a distance. To convert angle to distance, recall that at an angle Θ in a circle of radius r subtends distance rΘ at the edge of the circle (when Θ is measured in radians). Thus we can approximate 2 sides of the infinitesimal area as being of length Δr and the other 2 as being length rΔΘ, for total area r Δr ΔΘ.
Application
I think (but I expect everyone is too wise to listen to me on this) that Geneseo’s new library should be a mostly rectangular building, but with a big circular tower at the center of the front. The only reason for the tower is so that a glassed-in study area can wrap around the front half of it. The study area should have a curved wall/roof whose height above floor level is given by
h = √(4-r2)
where r is the distance from the center of the tower, in units that are totally made up, for the sole purpose of making the arithmetic in this problem easier. Whatever those units are, the tower proper has a radius of 1 unit, so the study area extends from r = 1 out to r = 2.

What is the volume of this study area? We’ll talk about this tomorrow. Start thinking about it in the meantime.
Next
Find the volume of the study area.
No new reading.