Lagrange Multiplier Examples

Return to Course Outline

Previous Lecture

Problem Set

On directional derivatives, gradients, and our recent applications of partial derivatives.

See the handout for details.

Grading for this is Monday through Wednesday the week after next (April 13 through 15).

Notice that this is the first individually graded assignment. You may work on it in groups, but each person has to come explain it to me and get questions answered individually.

Lagrange Multipliers

Section 13.8 in the textbook.

2-Variable Example

The example we started yesterday: Find the maximum value of f(x,y) = x² - 4x + 4 + y², subject to the constraint that x² + y² = 1.

Yesterday we took this as far as setting up the Lagrange multiplier equation involving ∇ f and ∇ g, breaking that apart into separate equations involving x, y, and λ, and starting to solve those equations:

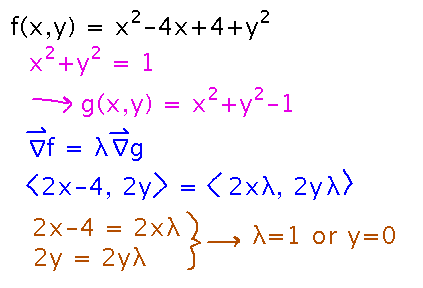
Finish solving this problem.

The first observation is that if you plug λ = 1 into the equation for the x components of the gradients, you get -4 = 0, which is impossible.

So it must be the case that y = 0. Plug this into the constraint to find x (you get 2 values), and then plug those and y = 0 into f(x,y) to decide where the maximum and minimum are:

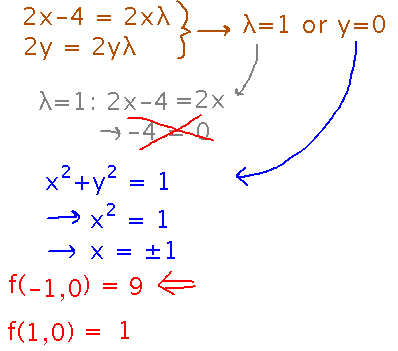
3-Variable Example

The “Cobb-Douglas function” from the book: f(x,y,z) = x^0.2y^0.4z^0.4.

Cobb-Douglas functions are a family of functions used in certain economic models of how output from some business or industry depends on inputs, originally of labor and capital, but also perhaps other things. The variables represent the various inputs, the function’s value represents the amount of output produced.

Suppose you want to maximize this Cobb-Douglas function subject to the constraint that x + y + z = 1. Use Lagrange multipliers to do so.

The first step, as in all Lagrange multiplier problems, is to find the gradients, and put them into the Lagrange multiplier equation:

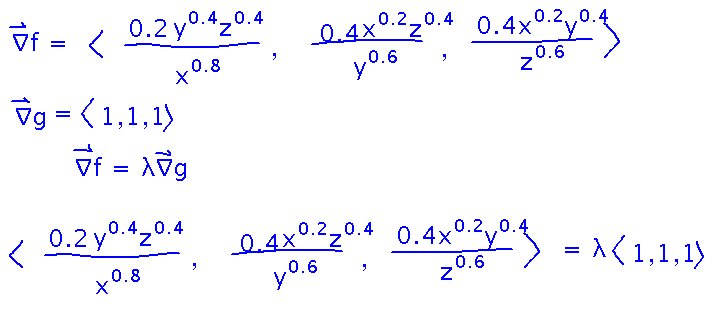
In this particular problem, we end with all 3 components of ∇ f equal λ, which means they all equal each other. We can then use pairs of them to find relations between x, y, and z. (Or use all 3 at once to find the same relations a little faster but in maybe a less obvious way.)

Notice that this involved dividing by variables, and thus dividing away solutions in which those variables are 0. In this problem, all such solutions can be ruled out because of the nature of the problem, namely that the Cobb-Douglas function produces a non-negative result, and becomes 0 when any of the variables are 0; 0 is more likely to be a minimum than a maximum of a non-negative function (though we should keep the 0 in mind in case everything else we find later in this problem also leads to f(x,y,z) = 0).

Finally, plug the relationships we’ve found between x, y, and z into the constraint to find exact values for x, y, and z:

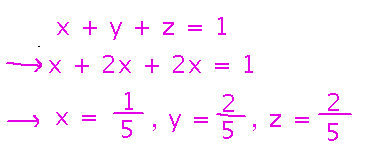
Next

Integrals of multivariable functions.

Read “Volumes and Double Integrals,” “Properties of Double Integrals,” and “Iterated Integrals” in section 14.2.

Next Lecture