Multiple Integrals over Rectangular Regions

Return to Course Outline

Previous Lecture

Questions?

Multiple Integrals with Rectangular Regions

“Volumes and Double Integrals,” “Properties of Double Integrals,” and “Iterated Integrals” in section 14.2.

Key Ideas or Questions?

A double integral is the volume underneath a surface — i.e., the (signed) volume between the xy plane and the surface, analogous to a single-variable integral being a (signed) area under a curve.

A double integral is therefore a double Riemann sum, a sum of volumes of rectangular solids.

Lots of the algebraic properties of single-variable integrals then extend to multivariable integrals.

But you can evaluate a double integral as an “iterated integral,” i.e., an integral of an integral. You don’t need to do it as a Riemann sum.

Iterated integrals can generally be evaluated in whatever order makes them easiest.

Introduction

Evaluate the integral over the region R = [0,π/2] × [π/2,π] of cosx cosy.

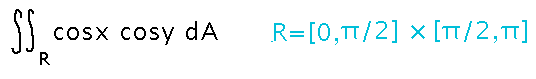
Write this as an iterated integral. Notice how the integral symbols and differentials balance from inside to outside, to truly make this an integral evaluated inside another integral.

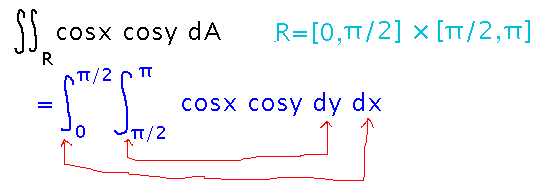
Now evaluate the integrals from innermost to outermost. Along the way, you could if you wished simplify the problem into a product of integrals (the textbook’s Property VI, one of the few double integral properties that doesn’t have an analogous single integral property).

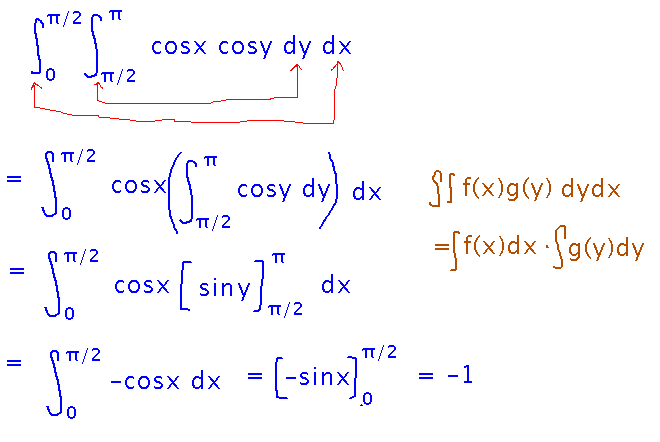
Order of Integration

Evaluate the integral over the region R = [0, ln3] × [0,1] of x e^2xy.

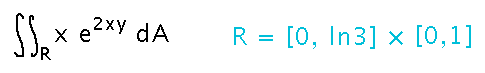
Here the main thing is what order you evaluate in, i.e., whether the integral with respect to y is the inner one, or the integral with respect to x. Taking the inner integral with respect to y looks like it will just need a substitution to evaluate, whereas taking the inner integral with respect to x seems to call for integration by parts.

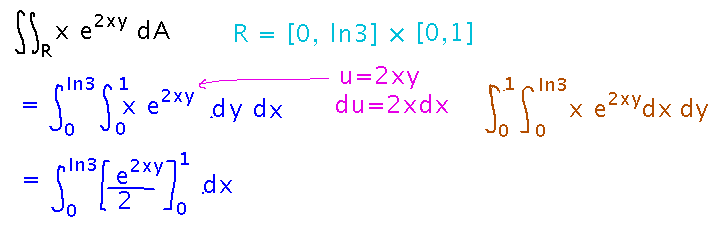
Next

Finish the above integral of x e^2xy. Try integrating at least one of the beginnings all the way to a number for yourself before Wednesday.

Look at another example.

Start talking about applications of multiple integrals.

No new reading, although “Applications of Double Integrals” in section 14.2 will be a preview of things we’ll start talking about (and it will probably be assigned reading for Thursday).

Next Lecture