SUNY Geneseo Department of Mathematics

Introduction to Directional Derivatives

Wednesday, March 25

Math 223 01
Spring 2020
Prof. Doug Baldwin

Return to Course Outline

Previous Lecture

Misc

Syllabus changes. See the revised syllabus in Canvas.

Tests

I have decided to replace the second hour exam and final with individually-graded problem sets.

All problem sets after the one I’ll hand out today (Problem Set 10 on partial derivatives) will be “individually graded.”

The only difference between an “individually graded” problem set and previous ones is that you must meet individually with me to grade them, and you should expect that in that grading I will ask more questions getting at how well you understand the ideas behind your answers. You can still help each other with “individually graded” problem sets though.

Grading

Weights on problem sets have changed, to distribute the 70% originally assigned to exams over them. See the syllabus for details.

I’ve assigned “participation” grades based on participation during the face-to-face part of the course. Because people may face idiosyncratic and uncontrollable barriers to traditional participation during the remote learning part, I don’t plan to grade for participation from here on.

Recorded Class Sessions

Find them in Canvas’s “Blackboard Collaborate” window.

Pull down the menu in the upper left part of the window, select “Recordings”.

Problem Set

...on partial derivatives.

Grading next week, Wednesday and Thursday (April 1 and 2).

See the handout for details.

Questions?

Problem set question about defining what it means for a 2-variable function to have an infinite limit: for the limit in the question (limit as (x,y) approaches (0,0) of 1 / (x2+y2)), what shape is the size-δ region around (0,0)?

The idea is that at all points within distance δ of (0,0), f(x,y) has to be bigger than M. “All points within distance δ” suggests a circle:

Circle of radius delta in x, y plane with function shooting up above circle

Then you want to see if f(x,y) being bigger than M lets you somehow conclude that x2 + y2 is less than something, because if you can that “something” is δ2.

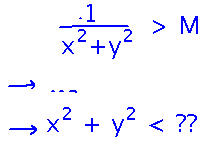
From 1 over x squared plus y squared greater than M, conclude x squared plus y squared less than something

Directional Derivatives

“Directional Derivatives” in section 13.6.

Key Idea(s)

Directional derivatives are slopes of tangent lines that don’t need to be parallel to the axes.

There are formulas for directional derivatives in terms of limits, and in terms of regular partial derivatives

Basic Definition and Formula

Use the limit definition to find the derivative of f(x,y) = x2 + y2 + 2x + y in the direction π/6 radians (30 degrees) towards the y axis from the x axis.

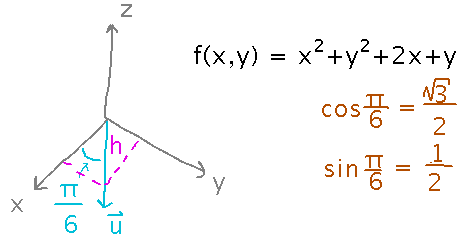
Direction vector at angle pi over 6 from x axis, function x squared plus y squared plus 2 x plus y

Start with the basic limit definition. Notice that it basically looks like every other derivative definition, i.e., a limit involving a small change in the inputs to a function. The sine and cosine in the definition of a directional derivative serve to assign part of that change to x and part to y, according to the direction in which the “small change” is happening.

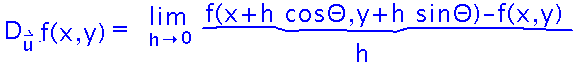
Limit definition of derivative of f in direction u

Now plug in the specific function and sine and cosine, and do a lot of simplifying:

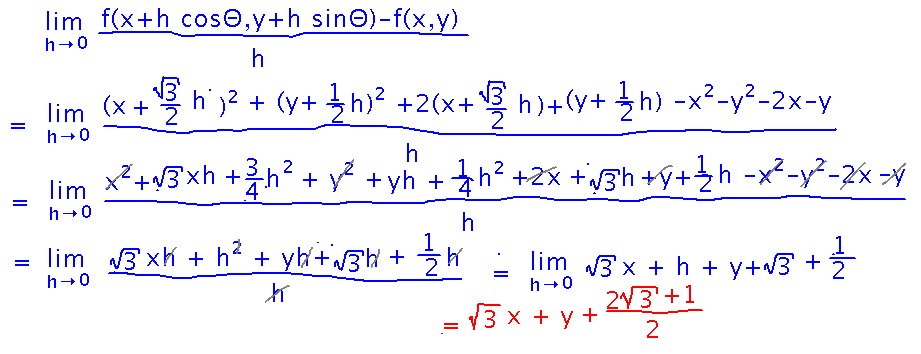
Expand terms in limit definition, cancel, and set h to 0

Next

Directional derivatives beyond the limit definition.

No new reading.

Next Lecture