More about Directional Derivatives

Return to Course Outline

Previous Lecture

Misc

Extra Credit Opportunities:

• The Geneseo Insomnia Film Festival has been canceled for this year, but I did offer up to half a problem set extra credit to people who take part in making a movie with some sort of math-based plot (but not a tutorial). That offer still stands.
• The “real-world math bounty” (write up a short description of how some idea from this course applies to something outside the course in your own, or your acquaintances’, life) is still available.

Questions?

Will individual problem set grading appointments have a longer grading window than previous problem sets?

We’ll see how things go. I’m hoping we can grade in 15 minute appointments once people get used to doing it online. In principle, there are enough 15-minute appointments in a 2 day window to fit everyone in. But it might also turn out that more flexibility re times is desirable even so.

I will cut back a bit on the frequency of problem sets, so there will be more time in my schedule to go to, for example, 3-day grading windows if that turns out to be helpful.

Directional Derivatives

The “Directional Derivatives” subsection of section 13.6 of our textbook.

Partial Derivative Formula

Yesterday we used the limit definition of a directional derivative to find that for f(x,y) = x² + y² + 2x + y, D_uf(x,y) = √3x + y + (1+2√3)/2 where u is a unit vector at a π/6 radian angle from the x axis.

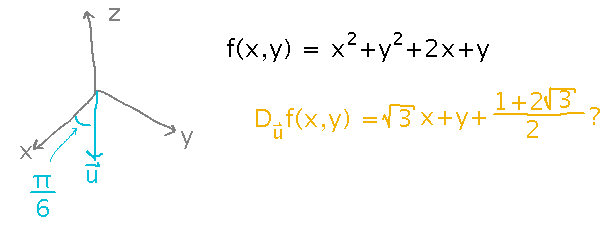
Check that result by using the formula for a directional derivative in terms of partial derivatives.

Plug the derivatives of f with respect to x and y, along with the sine and cosine of the angle, into the formula, and simplify:

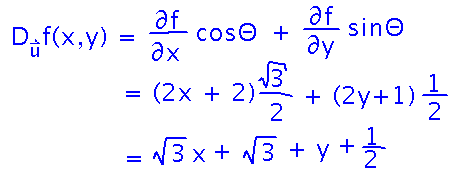
Although it’s hard to see how this formula could extend to more than 2 dimensions, directional derivatives are in fact defined for functions of any number of variables. The tricks are (1) that the sine and cosine terms we have used can actually be cosines of angles between the direction vector and each axis (e.g., our sinΘ could actually be the cosine of the angle between u and the y axis), and (2) there are other formulas that are more obviously independent of the number of dimensions (notably a gradient-based formula we’ll see tomorrow).

Direction as a Vector

Given h(x,y) = sin(x²) - 3xy², find the derivative of h in direction u = ⟨ 2,1 ⟩.

Use definitions of trigonometric functions to find the sine and cosine from the sides of a right triangle whose hypotenuse is the direction vector. Then use the same formula as earlier.

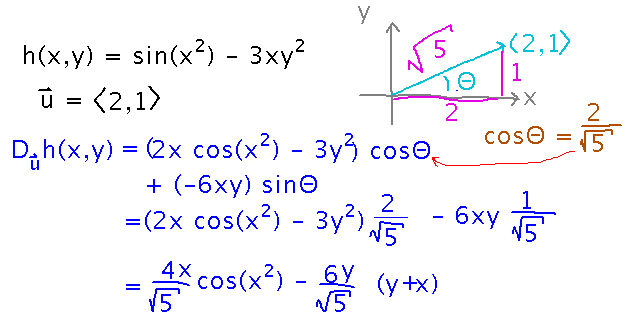
Notice that finding the sine and cosine is exactly equivalent to scaling the direction to a unit vector and then using its components in the directional derivative formula.

Application

Imagine a coordinate system whose x axis points south, y axis east, and z axis up. There is a hill in this coordinate system whose elevation at point (x,y,z) is given by z = 10 - x² - y². All distances are measured in meters. Suppose you’re standing at point ( -1/2, -1/2, 9 1/2 ) on this hill, walking northwest. How fast is your elevation changing, i.e., how many meters do you rise or fall per meter walked horizontally?

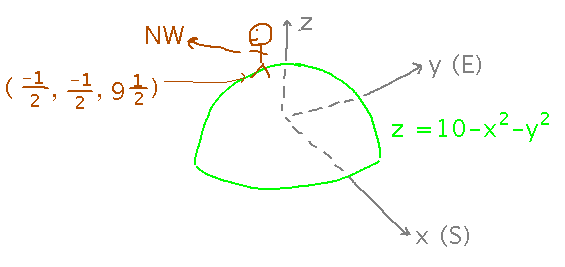
Start by getting a direction vector or angle:

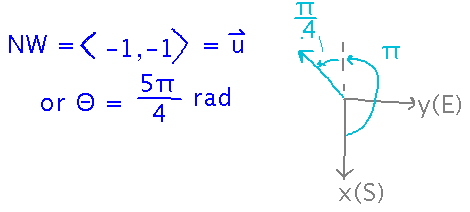
Plug the direction and derivatives of z into the directional derivative formula, and evaluate at x = -1/2, y = -1/2:

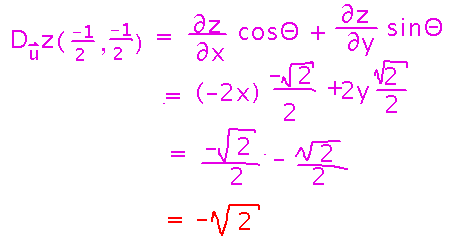
(Canceled) Field Trip

If we were meeting face-to-face, we would go outside and use hilly parts of campus to demonstrate the idea that rate of change can depend on direction.

We can’t do that as a group, but I’ve set up a discussion where you can take yourself on a private field trip and post photos if you want.

But only if you can do it safely, and feel like it. This isn’t graded or counted for credit in any way.

Next

Gradients: another way of approaching directional derivatives, and a concept that provides useful ways of working with partial derivatives in its own right.

Read “Gradient,” “Gradients and Level Curves,” and “Three-Dimensional Gradients and Directional Derivatives” in section 13.6.

Next Lecture