Back from Break — To Remote Learning

Return to Course Outline

Previous Lecture

Misc

Welcome Back

Summary of Plans for the Course

We “meet” at our regular time (MWRF 1:30) via Blackboard Collaborate’s “course room.”

Meetings will be recorded for people who want to watch them later, and summarized in Canvas pages (like this one) for people who want a mainly textual version.

Problem sets are the focus of the learning; we’ll keep doing them and grading them one-on-one via video meetings (Blackboard Collaborate, at least to start with).

For grading “meetings,” you will need to have a solution ready to show me on the computer -- that could be a Word document, Google doc, photo of handwritten solution, etc. But it needs to be on a computer and sharable, and ideally there will only be one, even if you have a group solution.

I can enable you to share things through Blackboard Collaborate.

Tests

I’m wondering what to do about the second hour exam and final. I definitely want to keep assessment focused on your ability to use ideas from this course in new problems. Possibilities include...

• We could maybe just about do something close to a proctored exam through a combination of lockdown browser and/or video monitoring, though fully open-references might be hard, real proctoring might be hard, and turning in solutions might be hard.
• Unproctored take-home exams on an honor system.
• We could replace the remaining exams with the remaining problem sets (plus maybe one more at the end of the semester) with more attention to how well you understand your answers during grading.
• Most problem sets could stay regular problem sets, but a few become “exam problem sets” where grading focuses more on your individual understanding, maybe group work isn’t allowed, time frames might be slightly shorter, questions might be more about past material than current, etc.

While this isn’t a vote, I am interested in any thoughts, preferences, or questions you have. There was considerable sentiment in favor of something focused on problem sets rather than trying to recreate “classical” exams.

Speaking of Thoughts, Preferences, or Questions...

There’s a mid-semester feedback survey on Canvas that you can use to give me anonymous feedback on how this course is working for you so far.

I’d be particularly interested in any ideas you have about how to make this course most effective in “remote learning” mode.

Other Tips

Blackboard Collaborate etiquette suggestions:

• Mute your microphone except when you want to say something (this avoids background noise from your location transmitting to other people, and maybe damping of another speaker when BC thinks you’re speaking). The practice you’ve developed of raising electronic hands when you want to speak and then waiting to be recognized is also working well.
• Mute your camera to save network bandwidth.

For Macintosh users, Blackboard Collaborate might provide more functionality through Chrome than Safari.

For consistency with past practice, I will generally use lecture notes and Canvas announcements for course-related notices. You can set your personal Canvas account to email announcements to you if you wish.

Any time anything isn’t working for you, or you have a thought about how it could work better, or you just want me to know something, tell me! Flexibility is key.

Questions?

How to interpret and start the problem set question about the formal definition of an infinite limit?

The formal definition for one dimension captures the idea that “lim_x→a f(x) = ∞” means that f(x) gets unboundedly big as x approaches a. Specifically, no matter how big a bound you think you can set (M), there is some region of x values near a in which f(x) is even bigger.

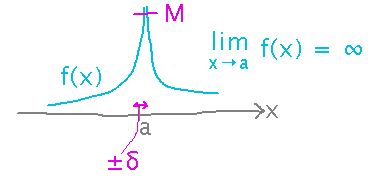
Typically you don’t pick or find a value for M. The idea is that it can be anything, so you have to find a general argument that shows for every M there is a δ interval around a within which f(x) is bigger than M.

But looking at how that would work for a few concrete examples of M can get your thinking started. For example, consider lim_{x → 0+} 1/x, which is a favorite example of an infinite limit:

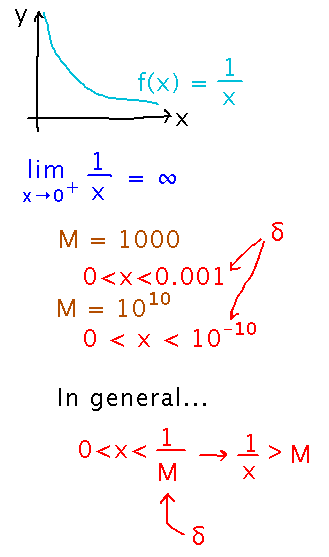
For the 2-variable case in the problem set, the main challenge is probably to generalize the 1-variable definition to multiple variables. Looking at how the textbook generalizes the 1-variable formal definition of a finite limit to multiple variables might give you some ideas.

Next

Directional derivatives.

Read “Directional Derivatives” in section 13.6.

Next Lecture