Partial Derivatives

Return to Course Outline

Previous Lecture

Misc

I’ll be out of town much of next week: Tuesday afternoon through the end of the week.

I’ll devise some sort of online activities for Wednesday, Thursday, and Friday classes (maybe class via video chat Wednesday and asynchronous discussion activities for Thursday and Friday).

Questions?

Derivatives of Multivariable Functions

First 2 subsections of section 13.3 in the textbook.

Key Idea(s)

“The” derivative doesn’t make sense for a multivariable function, but derivatives with respect to specific variables do make sense. These are called partial derivatives.

To take a partial derivative with respect to x, treat all variables other than x as constants.

Notations: ∂f/∂x or g_x(x,y).

Partial derivatives have a limit definition that is a generalization to multiple variables of the definition for single-variable functions.

Limit Definition

Use the limit definition to find ∂f/∂x and ∂f/∂y where f(x,y) = x² - xy + 2y.

For the derivative with respect to x, start with the definition itself, plug in the expression for f, and expand and simplify:

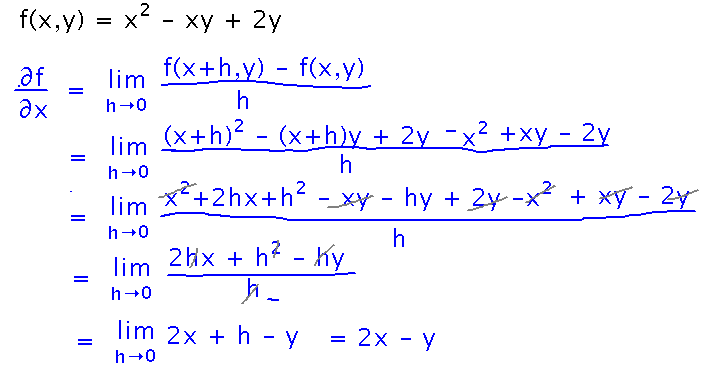
Then do similarly for y:

Differentiation Rules

Given g(x,y) = xy / (x² + y²), find g_x(x,y) and g_y(x,y).

Use differentiation rules, notably the quotient rule. The main trick here is to remember that when those rules call for “the” derivative of something, that means the derivative with respect to whatever variable you’re currently working with.

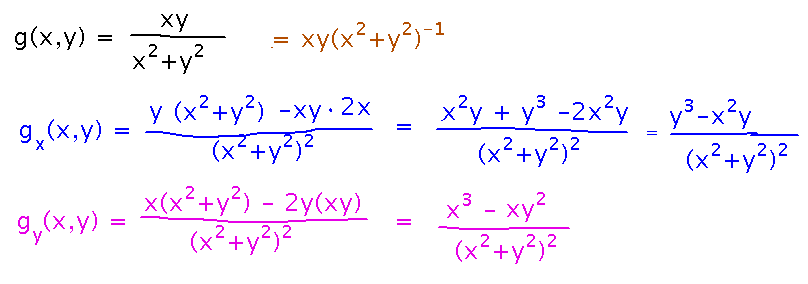
Partial derivatives with respect to different variables aren’t always as similar as in the previous example. For example, let h(x,y) = x^y, and find ∂h/∂x, ∂h/∂y.

You really can believe the “treat other variables as constants” rule, and find these derivatives with the power rule and general rule for exponentials:

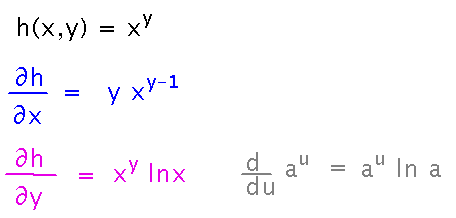
Problem Set

On limits of multivariable functions and a bit about partial derivatives.

See handout for details.

Next

Extensions to the idea (e.g., higher-order derivatives, finding derivatives with Mathematica, etc.)

Read “Higher-Order Partial Derivatives” in section 13.3.

Bring computers.

Next Lecture