SUNY Geneseo Department of Mathematics

More about Limits of Multivariable Functions

Wednesday, March 4

Math 223 01
Spring 2020
Prof. Doug Baldwin

Return to Course Outline

Previous Lecture

Misc

Colloquium on “Asymptotic Approximants”

Dr. Nate Barlow, RIT School of Mathematical Sciences

Wednesday, March 11, 2:30 - 3:30

Newton 209.

Extra credit for a paragraph on connections you make to the talk or reflections on it.

Questions?

Limits of Multivariable Functions

Section 13.2

Key Ideas

Limit laws, and techniques for using them, for multivariable functions are extensions of the laws and techniques for single-variable functions.

A limit does not exist if approaching along different paths yields different limits.

The definition of continuity for multivariable functions is the single-variable definition, using multivariable limits.

Limits that Do Not Exist

Show that lim(x,y)→(0,0) x/y does not exist. Consider x and y approaching (0,0) along different paths, and notice that each implies a different limit:

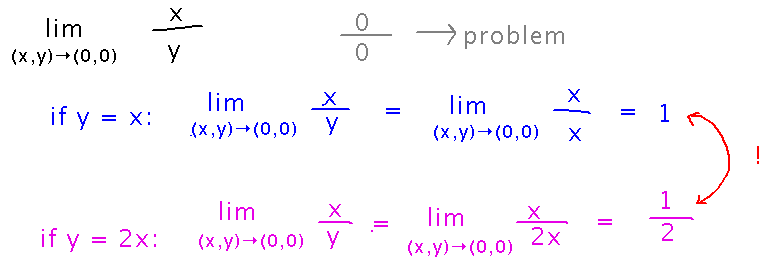
Approaching point 0, 0 on different paths leads to different limits for x over y

Why different limits on different paths imply that a limit as a whole doesn’t exist is similar to the single-variable case, where different limits from the left and right imply no two-sided limit. Also see the animation of different approach paths in the textbook.

Graph of a function with a break at x equals a

But note that unlike the single-variable case, having the same limit along 2 paths doesn’t imply that value is the limit. With multiple variables, there are infinitely many ways you can approach a point, rather than only having 2 like you do with only 1 variable.

Also notice that there’s no L’Hospital’s rule for multivariable limits.

Consider the book’s exercise 13.2.2: We found at least 3 paths along which to approach (2,1), all of which led to different limits:

Different ways of approaching point 2, 1 lead to different limits

Continuity

Is f(x,y) = (x2 - y2) / (x + y) if x ≠ 0 or y ≠ 0; f(0,0) = 1, continuous at (2,1)? Yes, it satisfies the 3 requirements for continuity, namely that f(2,1) is defined, the limit as x and y approach (2,1) is defined, and the limit and function value are equal:

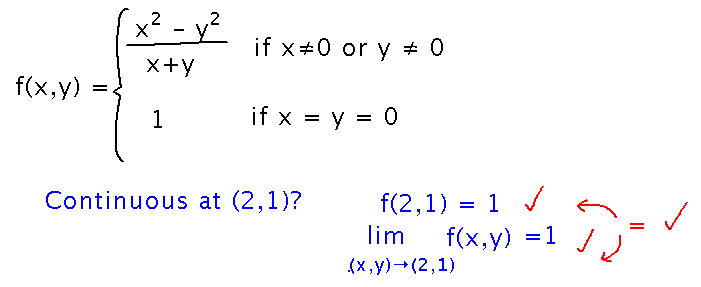
Function and limit both exist and are equal to 1

How about (0,0)? No. The function and limit are both defined, but aren’t equal:

Function is 1, limit is 0, so not continuous

Next

Derivatives of multivariable functions.

Read “Derivatives of a Function of Two Variables” and “Functions of More than Two Variables” in section 13.3.

Next Lecture