More about Partial Derivatives

Return to Course Outline

Previous Lecture

Misc

Try out Canvas’s “Blackboard Collaborate” video tool for Wednesday’s class (notice it towards the bottom of Canvas’s navigation bar).

Questions?

Mathematica and Partial Derivatives

Mathematica’s D function does partial derivatives. With multiple variables, find a higher-order derivative with respect to the variables in the order listed. With a list of variables in double brackets, give a vector of derivatives.

See this notebook for examples.

Higher-Order Partial Derivatives

“Higher-Order Partial Derivatives” in section 13.3.

Warning: Our book consistently interprets the “∂-” notation for partial derivatives backwards from how everyone else does it: to everyone else, ∂²f/∂x∂y means ∂/∂x (∂f/∂y).

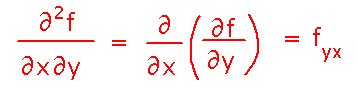
We will use the conventional notation (given above), not the book’s.

Key Points

Higher order derivatives are possible.

How to evaluate them and interpret the notation.

Derivative with respect to x and then y equals the derivative with respect to y and then x, as long as the second derivatives are continuous (Clairaut’s Theorem).

Example

Find all the second-order derivatives of z = 3x²y² + e^xy.

Start with the 2 first derivatives, then differentiate each of them with respect to each variable:

Does ∂³f/∂x²∂y make sense? Yes, it’s a 3rd derivative, the first derivative taken with respect to y, the second with respect to x, and the third with respect to x again.

Next

Tangent planes, etc.

Read section 13.4.

Next Lecture