Misc
Problem Set
...on derivatives and integrals of vector-valued functions.
See handout for details.
Hour Exam 1
Next Thursday (Feb. 27).
Covers material since the beginning of the semester (e.g., 3D coordinates, lines/planes/surfaces, vectors, vector-valued functions, their derivatives and integrals, etc.)
3 - 5 short-answer questions, similar to mid-difficulty questions from problem sets.
You’ll have the whole class period.
Open book, notes, calculator, computer as a reference or calculator. But closed person.
Questions?
Arc Length
“Arc Length for Vector Functions” and “Arc-Length Parameterization” in section 12.4.
Key Ideas
Arc length formula:
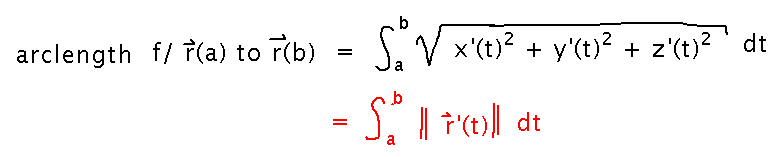
Arc Length
What is the length of r(t) = 〈 cos t, √3/2 sin t, 1/2 sin t 〉 as t ranges from 0 to 2π?
(The shape is a circle, angled with respect to the xy plane.) Find length by plugging the appropriate functions into the formula. Note that we can check the result against geometric formulas: the circle has radius 1, and so should have circumference 2π, which the arc length formula found:
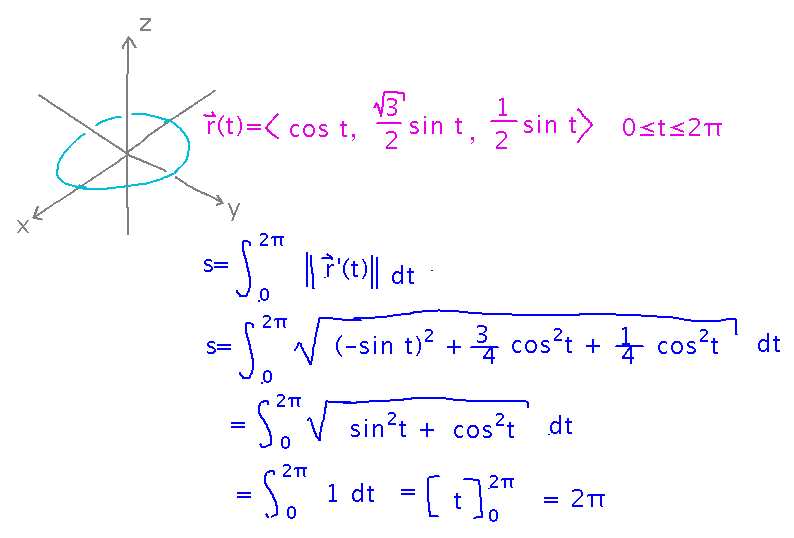
How about the length of p(t) = ⟨ t2+1, 2t2, t ⟩, 0 ≤ t ≤ 2?
Set this up according to the book’s formula, but then use Mathematica to evaluate the integral:


Mathematica is helpful for evaluating vector-valued integrals as well as scalar ones, both definite and indefinite (and derivatives, while we’re at it). Use the Integrate function to do both kinds of integral, and D to take derivatives. This notebook demonstrates, along with doing some other things that were helpful today.
With a way to find arc length, you can also do “arc-length parameterization,” re-parameterizing a function so that distance along the curve varies in 1-to-1 proportion to the parameter’s value.
Next
How sharply does a vector-valued function’s plot bend — curvature.
Read “Curvature” and “The Normal and Binormal Vectors” from section 12.4.