SUNY Geneseo Department of Mathematics

Curvature

Monday, February 24

Math 223 01
Spring 2020
Prof. Doug Baldwin

Misc

Hour exam 1 is Thursday (Feb. 27).

Covers material since the beginning of the semester (e.g., 3D coordinates, lines/planes/surfaces, vectors, vector-valued functions, their derivatives and integrals, etc.)

3 - 5 short-answer questions, similar to mid-difficulty questions from problem sets.

You’ll have the whole class period.

Open book, notes, calculator, computer as a reference or calculator. But closed person.

Questions?

Curvature

Second half (roughly) of section 12.4.

Key Ideas

Curvature measures how fast a function is changing direction, i.e., how sharply its curve is turning.

Definition: curvature is the magnitude of the derivative of the unit tangent with respect to arc length.

Formulas for curvature.

Normal and binormal vectors.

Sanity Check

What should the curvature of a straight line be? And why?

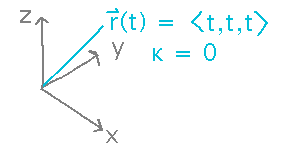
3 coordinate axes with line from origin at 45 degrees to each

Since a straight line doesn’t bend, the rate at which it’s bending must be 0.

Another way to understand curvature as a number is that curvature k is the rate at which a circle of radius 1/k bends:

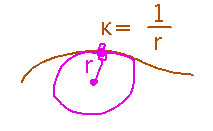
Circle of radius r nestles against curve of curvature 1 over r

Since radius would have to be infinite for a circle to be a straight line, the reciprocal is curvature 0.

Is that what the curvature formulas give for r(t) = 〈 t, t, t 〉?

Try finding curvature using the ratio of magnitudes of T’ to r’:

Calculating magnitude of T prime over magnitude of r prime

You can also find curvature using the cross-product formula:

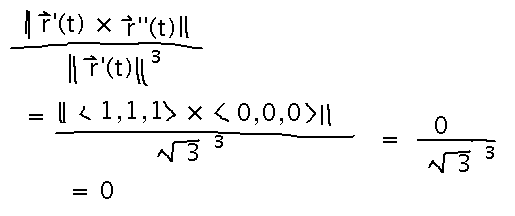
Calculating magnitude of cross product of r prime and r double prime over magnitude of r prime cubed

Both approaches agree with the informal analysis that the curvature is 0.

Example

Suppose r(t) = ⟨ -sin t, cos t, √3 t ⟩.

What’s the curvature? How about the principal unit normal?

Start by finding some building-blocks that we’ll want almost no matter what formulas we use, namely r’, T, T’, and some magnitudes:

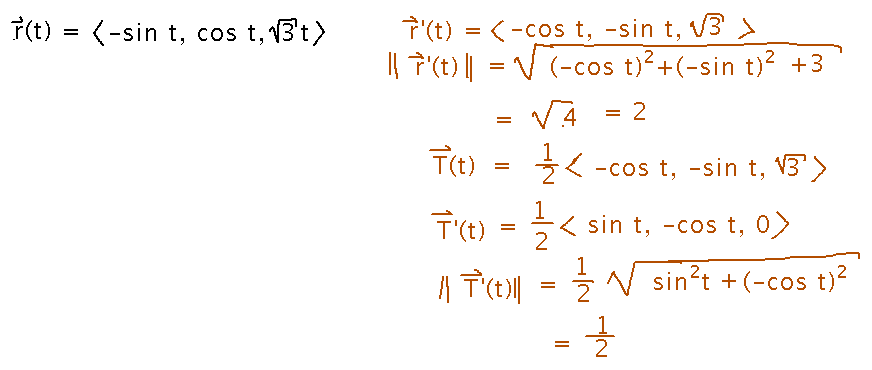
Vector formula and its derivative, unit normal and magnitudes

Now calculate curvature from the magnitudes of T’ and r’:

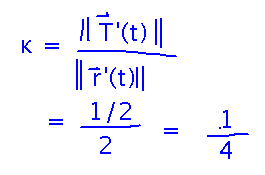
Calculating curvature as magnitude of T prime over magnitude of r prime

And calculate the principal unit normal from T’ and its magnitude:

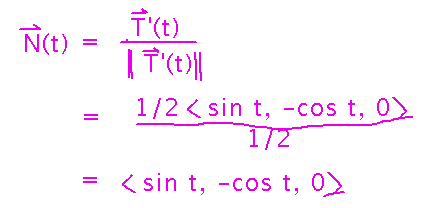
Principal unit normal is T prime over magnitude of T prime

Principal Unit Normal

As the name suggests, it’s normal, i.e., perpendicular, to the curve. But there is a whole circle’s worth of directions normal to a curve in 3 dimensions. Which one does the normal point in?

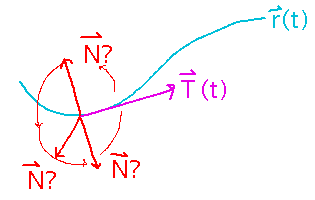
Curve with tangent vector; principal unit normal could be anywhere on circle around curve

We’ll start with this next time.

Curvature, principal unit normal, etc. as an excuse to try multi-step problem-solving with Mathematica.

Bring Mathematica to class!

Next Lecture