Misc
Hour Exam 1
Next Thursday (Feb. 27).
Covers material since the beginning of the semester (e.g., 3D coordinates, lines/planes/surfaces, vectors, vector-valued functions, their derivatives and integrals, etc.)
3 - 5 short-answer questions, similar to mid-difficulty questions from problem sets.
You’ll have the whole class period.
Open book, notes, calculator, computer as a reference or calculator. But closed person.
Questions?
Proving the sum limit law for problem set? A good way to do many proofs about limits of vector-valued functions is to move the limits inside the vector, use what you already know about limits of scalar functions, and then move the resulting limits back out of the vector.
Integrals of Vector-Valued Functions
Last subsection of section 12.2 in the textbook.
Key Ideas
The antiderivative of a vector-valued function is a vector of antiderivatives of components. Constants of integration form a constant vector of integration.
The definite integral of a vector-valued function is the vector of definite integrals of components.
The Fundamental Theorem of Calculus applies to vector-valued functions.
Example
Find an antiderivative and a definite integral. The key is to find antiderivatives and integrals of the components. And to remember that all the techniques of integration you know for scalar functions can be applied to the component functions.

Application
Once when I was lighting up an outdoor grill a fly flew over it and got killed by the heat. What trajectory did the fly then follow?
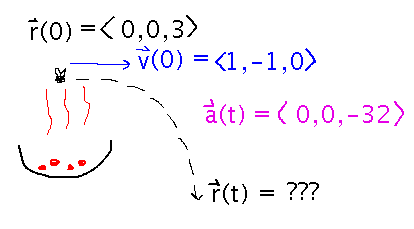
Start by integrating acceleration to get velocity, using the initial velocity to solve for the constant of integration:
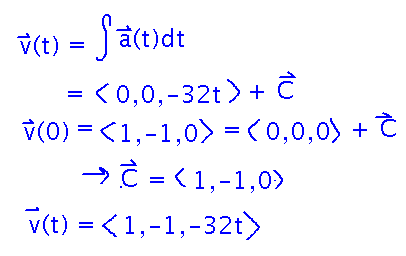
The similarly integrate velocity to get position:
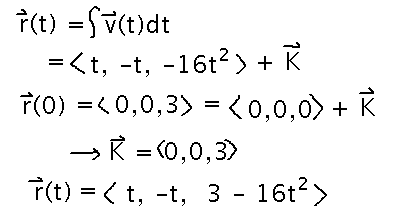
Next
Arc length of vector-valued functions.
Read “Arc Length for Vector Functions” and “Arc-Length Parameterization” in section 12.4.