Limits of Vector Valued Functions

Return to Course Outline

Previous Lecture

Misc

GROW STEM talk.

“Creating Climate Change in STEM”

Prof. Katelynn Kochalski

Wednesday, February 19, 2:30 - 3:30

Newton 214

Extra credit for attending and writing connections/reflections, as with colloquia.

Questions?

Parameterization / Reparameterization?

Vector-valued functions, whether defined piecewise or not, are always parameterized. That’s what “t” is.

Reparameterizing is when you change the parameter somehow while keeping the same curve. For example, we reparameterized our helix-and-line function Friday by changing the parameter to the helix part so it would range from 1 to 3π + 1 instead from 0 to 3π.

Other common examples of reparameterizing include switching to the so-called “arc length parameterization” (in which the parameter tells you how far along the curve you are from some starting point, in meaningful distance units), or reparameterizing to traverse a curve in the opposite of the original direction.

Piecewise Vector-Valued Functions

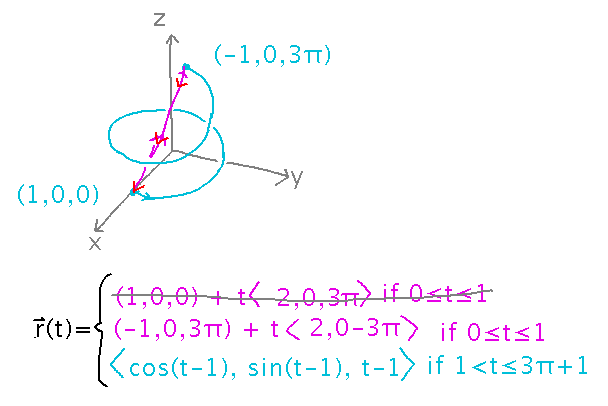
The piecewise vector-valued function we came up with Friday, whose graph was 1 1/2 turns of a helix with a diagonal line connecting the ends of that helix:

• r(t) = ( 1, 0, 0 ) + t 〈 -2, 0, 3π 〉 if 0 ≤ t ≤ 1
• r(t) = ⟨ cos (t-1), sin (t-1), t-1 ⟩ if 1 < t ≤ 3π + 1

As we defined this, it has a discontinuity at t = 1.

To “fix” this, arrange for the line part of the function to “grow backwards,” i.e., instead of proceeding from (1,0,0) when t = 0 to (-1,0,3π) when t = 1, have it go from (-1,0,3π) when t = 0 to (1,0,0) when t = 1. This just requires using (-1,0,3π) as the starting point in the line equation, and negating the direction vector:

Limits of Vector-Valued Functions

“Limits and Continuity of a Vector-Valued Function” in section 12.1

Key Idea

The limit of r(t) = ⟨ f(t), g(t), h(t) ⟩ is ⟨lim f(t), lim g(t), lim h(t) ⟩.

Example

Find lim_t→1 f(t) where f(t) = ⟨ (t²+t-2)/ (t-1), sin πt/2, t²/(t+1) ⟩

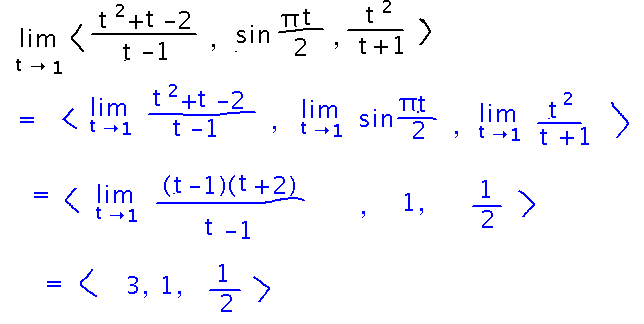
All the tricks you know for finding limits (L’Hospital’s rule, factoring to cancel a 0 denominator, etc.) work for the component functions of vector-valued functions.

Limits in Mathematica

Mathematica knows how to take limits, via the built-in Limit function.

See this notebook for an example.

Formal Definition

Draw a picture of the formal meaning of the limit of f(t) = ⟨ (t²+t-2)/ (t-1), sin πt/2, t²/(t+1) ⟩ found earlier.

The key thing is that the formal definition of limit in this case is based on the distance between 2 vectors going to 0.

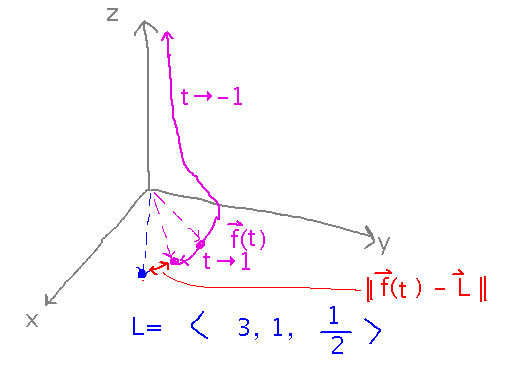
Also notice that the z component function has an asymptote at t = -1. This means that the curve of f(t) approaches a point whose z coordinate is infinite (even though x and y are finite) as t approaches -1.

Problem Set

On vector-valued functions and limits.

See handout for details.

Next

Derivatives of vector-valued functions.

Read “Derivatives of Vector-Valued Functions” and “Tangent Vectors and Unit Tangent Vectors” in section 12.2.

Next Lecture