Misc
Colloquium: “Evolutionary Games We Play: Hawks, Doves, and More”
Prof. Ted Galanthay, Ithaca College
Thursday, February 20, 2:30-3:30 pm, Sturges 109.
Extra credit for a paragraph on connections, reflections, etc.
Questions?
The first example in the reading has an inexplicable expression in it. This was a typo in the book, a fix for which was working its way to the book as we spoke (it’s corrected in our book now).
Derivatives of Vector Valued Functions
First parts of section 12.2.
Key Ideas
Derivatives of vector-valued functions have the same limit definition as derivatives of scalar functions, but with vectors.
The derivative of a vector-valued function is a vector of derivatives of the component functions.
The derivative is a vector tangent to the function’s curve.
The principle unit tangent vector gives the direction of the tangent aka derivative.
Example
(Similar to example 12.2.2)
Find the derivative of r(t) = 〈 3t - 1, √(t2+4), ln t 〉
Differentiate each component function. Note that you can use all the rules you know for taking derivatives, e.g., the chain rule, product and quotient rules, etc.
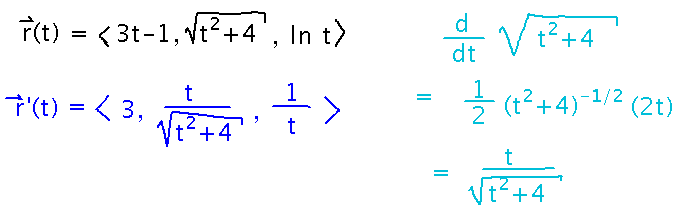
You could also use the limit definition of the derivative to solve this problem, although that’s longer and more tedious than the above.
Application
Imagine swinging a weight on a string along the helix h(t) = ⟨ 2 cos t, 2 sin t, t ⟩.
(Similar to Example 12.2.3)
What is the velocity vector for the weight?
What is its speed?
Velocity is the derivative of acceleration. Speed is the magnitude of velocity. Physically, velocity tells you how fast the weight is moving and in what direction (speed just tells you how fast).
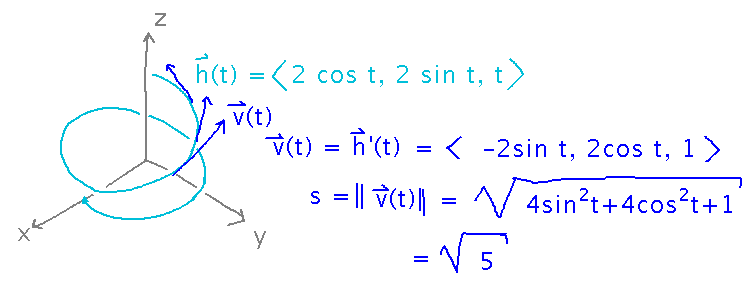
(Not similar to any example)
If I want to release the weight so that it flies away in direction ⟨ -√(2/5), √(2/5), √(1/5) ⟩, when should I release?
The key idea is that the given vector is a unit vector with a specific direction; the velocity also has a specific direction, and you want to release the weight when the velocity has the same direction as the one you want. But the velocity vector isn’t necessarily a unit vector. To make the direction of velocity easier to compare to the desired direction, use the “principal unit tangent vector,” i.e., a unit vector with the same direction as the velocity. Then solve for the t value(s) that give the desired direction:
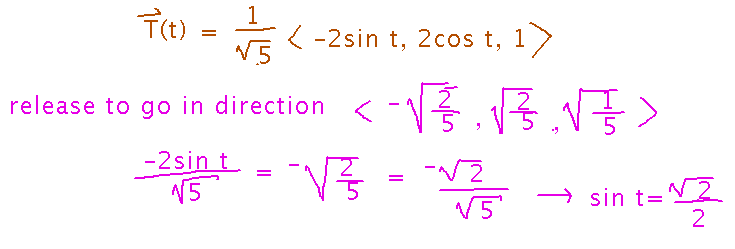
Next
Integrals of vector-valued functions.
Read “Integrals of Vector-Valued Functions” in section 12.2.