Questions?
Planes
Second half of section 11.5.
Equations
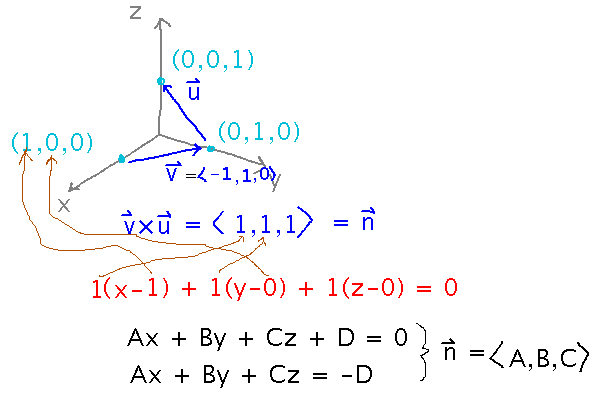
Yesterday we considered finding the plane that contains points ( 1, 0, 0 ), ( 0, 1, 0 ), and ( 0, 0, 1 ). By taking the cross product of two vectors between pairs of these points, we found a vector of coefficients for the plane equation, namely 〈 1, 1, 1, 〉. How come this vector gives the coefficients, and what does the equation actually look like?
Why: v × u is perpendicular to the plane, i.e., it’s a normal to the plane. The plane equations were built around the idea of the dot product between the normal and vectors to any point in the plane being 0:
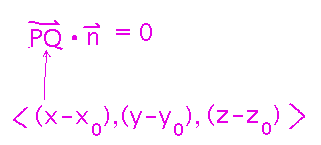
The complete plane equation comes from using components of the normal as coefficients, and components of any point in the plane as x0, y0, z0:
How about the plane perpendicular to r(t) = (1,2,3) + t ⟨ 2, -2, 1 ⟩ and containing point ( 2, 1, 5 )?
Here you have the normal vector already, from the line’s direction vector. Combine that and the point to get the plane equation:
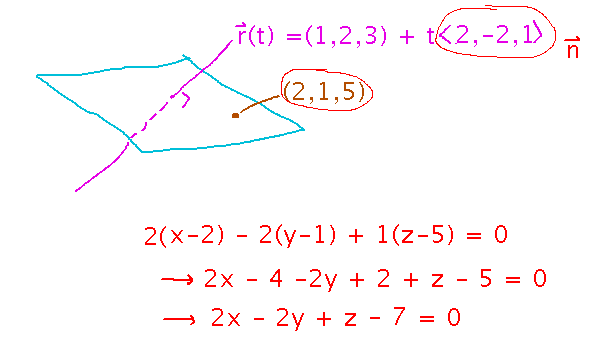
Using the Equations
Find one new point in the second plane above.
Just find any x, y, and z, by any means you like, that satisfy the plane equation.
Picking 2 variables arbitrarily and solving for the 3rd is the easiest way to do this:
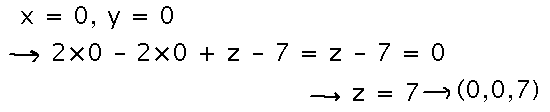
Line-plane intersections are useful, among other places, for “ray tracing” in computer graphics: mathematically trace backwards along rays of light reaching a virtual eye in order to find out where they came from and therefore what color they are.

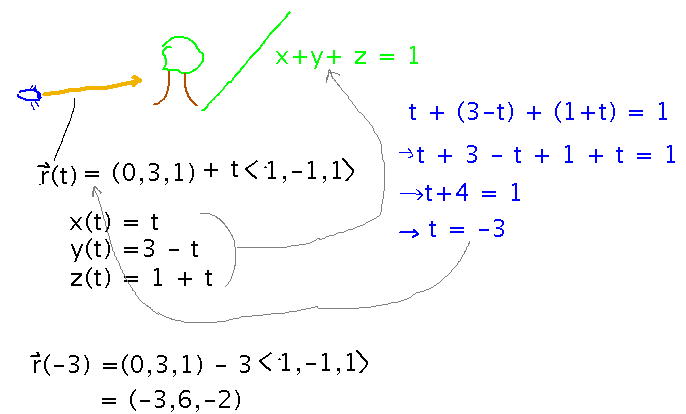
For example, suppose light arrived along the line r(t) = ( 0, 3, 1 ) + t ⟨ 1, -1, 1 ⟩ , and the plane x + y + z = 1 represents a hillside. Where (if at all) does the line intersect the plane?
Plug the parametric equations for x, y, and z into the equation for the plane, and solve for t. Then put that t back into the equation of the line to find out the actual point:
Problem Set
See handout for details
Next
Vector-valued functions
Read...
- Definition of a Vector Valued Function
- Graphing Vector Valued Functions,
- Finding a Vector Valued Function to Trace Out the Graph of a Function y = f(x)
- Finding a Vector Valued Function to Trace Out the Graph of an Equation in x and y and Vice Versa
- Parameterizing a Piecewise Path
in section 12.1