SUNY Geneseo Department of Mathematics
Wednesday, February 12
Math 223 01
Spring 2020
Prof. Doug Baldwin
Second half of section 11.5.
The notion of a “plane” can be defined by a set of vectors perpendicular to another vector.
(This turned out to be the main focus of today’s class.)
It really helps to consciously ask yourself questions (and answer them) about each sentence: what is this saying? does it make sense?
For equations and mathematical notations, ask whether you’ve seen the variables before, and if so, what they represent. If not, they’re being defined, so ask and note what they now represent.
Create mental images or examples of the ideas expressed in the text.
As soon as you come to something you can’t understand, or ask yourself a question you can’t answer, you have a question to bring to class. I expect this to happen -- even though I ask you to read before class, that doesn’t mean I expect every part of the reading to be clear.
If you don’t want to bring questions to class, consider emailing them to me before class so I can put them on the agenda anonymously.
Exercises in the text can be used for any of several purposes: to confirm you understood previous examples, to force yourself to deal with examples you didn’t quite understand, to save for practice before tests, etc.
Similar to example 11.5.5: Find an equation for the plane that contains ( 1, 0, 0 ), ( 0, 1, 0 ), and ( 0, 0, 1 ).
Start by finding two vectors between pairs of points:
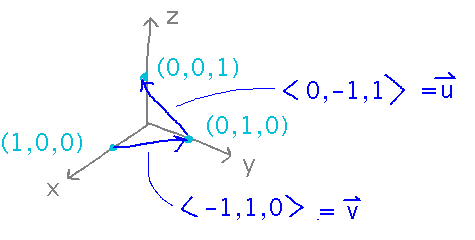
The cross product of those vectors gives you coefficients for the scalar plane equation.
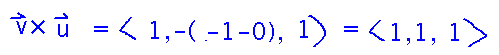
We’ll start tomorrow by talking about why this is, and writing down the equation.
Planes.
Re-read the second part of section 11.5, using the tactics we talked about today.