More About Lines

Return to Course Outline

Previous Lecture

Misc

Problem set on cross products (and dot products and lines a little bit).

See handout for details.

Questions?

What exactly are the vectors in question 3 on the current problem set? And what is the question asking?

One vector is a video game character’s “right” vector, and the other is the velocity of some object in the game. The question asks you to find the magnitude of the projection of that velocity onto the “right” vector.

Lines

First half of section 11.5.

Key Points

There are equivalent vector and parametric equations for lines.

You can use those equations to find, e.g., intersections of lines, distances from a line to a point, etc.

Equations

Find an equation for a line through points P( 2, 1, 1 ) and Q( 3, -1, 4 )

Start by finding a vector, v, from one point to the other. This vector gives you the direction the line goes in. Then imagine yourself walking along the line. You’d start at some point, so pick one that’s convenient, say point P. Then you walk along the direction vector; after t time units walking, you’d be t times that vector away from the point you started at. So the vector equation for a line captures these ideas by representing the line as a point (where you start walking) plus t times a direction vector.

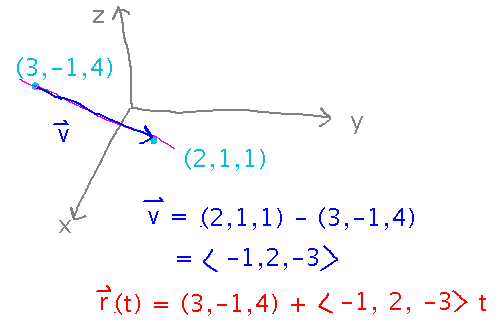
You can also capture these ideas in a more traditional set of parametric equations:

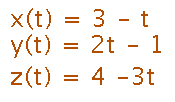
Are there any other equations for the same line?

Yes, you could use any other point on the line, or any multiple of the direction vector.

Applying the Equations

Do the lines r(t) = (0,1,0) + t⟨ 1, 1, 1 ⟩ and q(t) = (2,0,1) + t⟨ 0, 3, 1 ⟩ intersect? If so, where?

Similar to example 11.5.4

Since we just want to know if any point is on both lines, start by giving each line its own parameter (t and s) for its vector equations. Then see if there are values of the parameters that make the x, y, and z components of the two equations equal. Finding these values involves solving a system of linear equations; if there is a solution, the lines intersect.

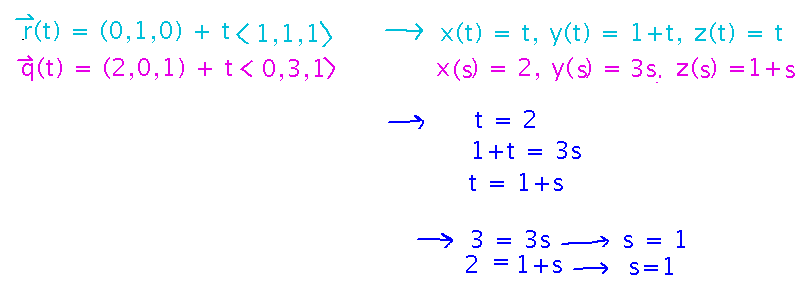
You can verify that the lines intersect by noticing that r(2) = (2,3,2), and q(1) = (2,3,2) also.

Next

Planes.

Read the rest of section 11.5.

Next Lecture