Questions?
Perpendicular Components
What’s with the reference that was once in yesterday’s Canvas notes to finding a vector’s “perpendicular component” relative to another vector?
Something I had lined up to talk about as an application of cross products if there was time. There wasn’t, but here’s a summary of the idea.
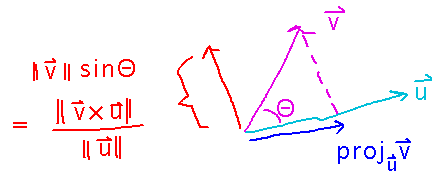
The idea is complementary to projection: when you project vector v onto vector u, you get a “component” of v that’s parallel to u. There’s also a component perpendicular to u, and together the parallel and perpendicular components add together to equal v. Just as the magnitude of the projection (parallel component) is calculated using a dot product because of the dot product’s connection to the cosine of the angle between 2 vectors, the magnitude of the perpendicular component can be calculated using a cross product, because of the cross product’s connection to the sine of the angle.
Up Vector Example
Review yesterday’s example where we calculated an “up” vector from “forward” and “right” vectors?
In order to draw first-person views of its virtual world, a video game might maintain vectors that describe the directions the player sees as “right” and “forward.” To produce a complete coordinate system for drawing what the player sees, the game also needs a vector that points in the player’s “up” direction. This vector can be calculated from the other two: since it has to be perpendicular to both, taking their cross product will do it. By the right-hand rule, doing the product as right cross forward makes the product point up (instead of down, which is the other choice):
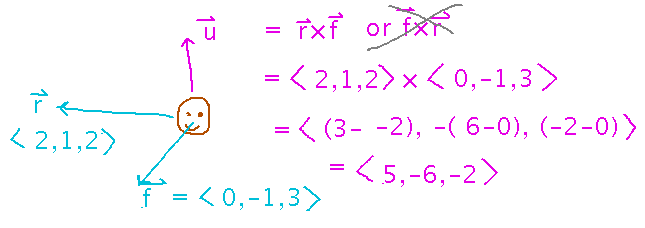
(Note that the vectors given in this example are good for demonstrating cross products, but totally wrong for an actual video game: from the x and y components they look like “right” points left more than right, and in any case they aren’t perpendicular.)
Lines
Why bother with section 11.5 on lines, when we’ve already seen equations that produce lines?
The equations we’ve seen are systems such as x =1, y = 7, which can produce lines parallel to the axes, but not at other angles. What we’re studying now produces lines at any angle.
Lines in Space
First half of section 11.5.
Basic Equations
Find an equation for a line between points (1,1,0) and (2,0,-2)
Start by subtracting one point from the other, to get a vector parallel to the desired line:

This vector tells you what direction the line goes in. Using it, you can build a vector (or parametric) equation for the points on the line. Think of this equation as giving a starting point, and then telling you where you’ll be if you walk t steps in the line’s direction — negative t means taking steps backwards, and t can be a fraction as well as a whole number.
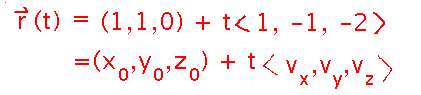
Don’t get distracted by the symmetric equation for the line. It’s a valid alternative form of equation, but probably not as useful as the vector equation. Despite looking like something you can solve to find t, it really isn’t, and t isn’t something you’d want to solve for anyhow, you want its value to vary in order to trace out the line via the vector equation.
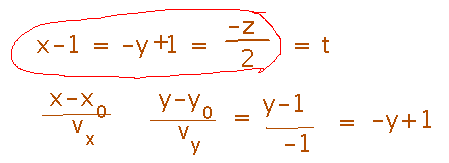
Next
More about lines.
No new reading (but reviewing the reading on lines would be good).