Questions?
Cylindrical Coordinates
First part of section 11.7.
Key Points
“Like polar coordinates with a z axis”
There are equations for converting to/from cylindrical/rectangular (based on trigonometry and Pythagorean Theorem - the important things to know are that the equations exist, and maybe enough about where they come from that you can quickly understand them when you see them - memorizing them isn’t particularly valuable considering how quickly you can look them up if you need them).
Example
The computer animated snake has coiled itself around a perfectly cylindrical tree of radius 1, aligned with the universe’s positive z axis, in such a manner that the snake’s nose is at ( -√2/2, √2/2, 5 ). Where is the nose in the cylindrical coordinate system defined by the tree?
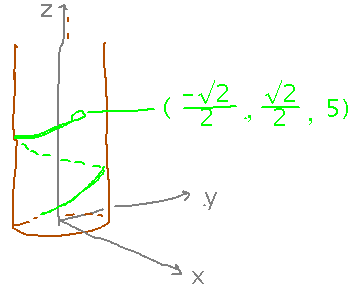
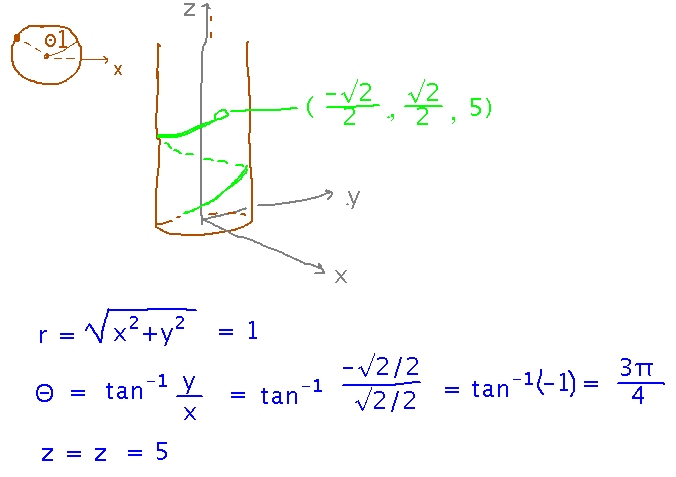
You can do some of this problem intuitively, e.g., knowing the radius of the tree tells you that the r coordinate must be 1, you can visually judge what angle would give x = -√2/2 and y = √2/2. But you can also do it more rigorously with the formulas for rectangular to cylindrical conversion:
The tip of the snake’s tail is 1 unit from the tree’s center, π/6 radians counterclockwise around the tree from the x axis, and 2 units up the tree. Where is the tail in rectangular coordinates?
Use the formulas for cylindrical-to-rectangular conversion to solve this:
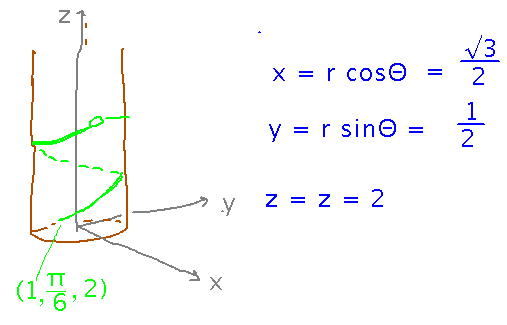
Spherical Coordinates
Second part of section 11.7.
Key Points
Spherical coordinates are an extension of polar coordinates with 2 angles (Θ counterclockwise from the x axis, Φ down from the z axis) and one distance (from origin).
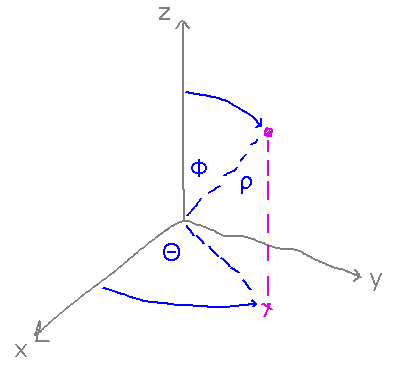
Beware of different notations in different disciplines.
There are equations to convert between spherical and rectangular.
Example
Geneseo is at latitude 43° N and longitude 78° W. Earth’s radius is about 4000 miles. What are Geneseo’s rectangular coordinates in a coordinate system whose origin is at the center of the Earth, whose x axis runs through the Prime Meridian, and whose z axis runs through the north pole?
There are 2 steps here. First, realize that latitude and longitude aren’t quite standard spherical coordinates. In particular, the angles are defined differently: latitude is an angle up from the equator, not down from the pole, and longitude may be measured either counterclockwise, if east, or clockwise, if west. So start by converting the problem description into standard spherical coordinates:
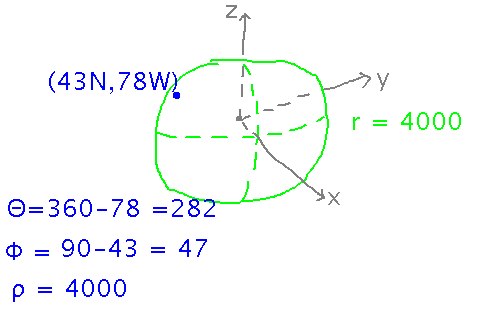
Then use spherical-to-rectangular conversion formulas:
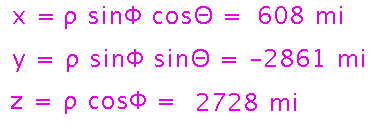
Next
Problem set, see handout for details.
Vectors in 3 dimensions.
Read “Working with Vectors in R3” in section 11.2.