Misc
For an introduction to scheduling appointments with Google calendar, see this video from CIT:
Also demo in class.
Questions?
Sphere Challenge
Why doesn’t Mathematica plot anything for my “sphere but with different coefficients” challenge from last class when all the coefficients are negative?
Because the x2, y2, z2 terms are necessarily positive no matter what values x, y, or z have. Multiplying them by negative coefficients produces a negative result, which can never equal positive 1. So these equations have no (real) solutions.
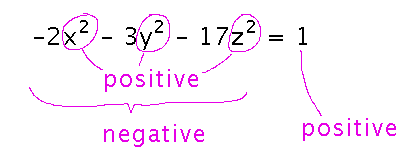
Hyperboloids
Discuss hyperboloids?
I find they’re easiest to understand if you start with hyperbolas in 2 dimensions:
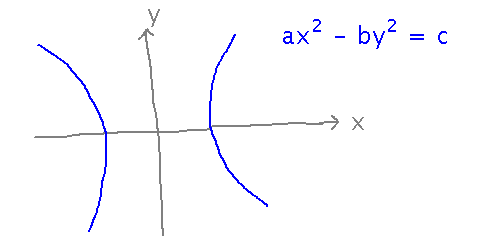
Then extend to 3 dimensions by subtracting a sum of y2 and z2. For any particular value of this sum, the combinations of x and y that produce that value will define an ellipse; thus the elliptical traces of the figure.
For each ellipse, there are two x values, one positive and one negative, that will satisfy the equation. But as x gets closer and closer to 0, eventually ax2 gets to be less than d, and there’s no sum of y2 and z2 you can subtract to get d (just like the missing plot in the previous question). Thus you get a gap between the two parts of the shape.

This is, of course, a hyperboloid of two sheets.
Sheets? One vs two sheets refers to the number of connected regions in the shape. I don’t know why the word “sheet” is used here.
Parabolic Reflector
Explain example 11.6.4?
Satellite dishes are paraboloids, because paraboloids have the property that TV signals arriving straight into the dish all reflect towards a single “focus” point. Putting the sensor that detects TV signals and sends them on to your television at that point will thus maximize the amount of signal it can pick up.
The example is about calculating where the focus is for a particular paraboloid.
It starts by simplifying the 3D problem into 2D. Since the paraboloid in question is circular (you know that because the coefficients of both x2 and y2 are equal), all cross-sections have the same shape, and so the focus for a 2D cross-section will be the same as the focus for the 3D surface. To simplify into 2D, consider just the trace of the paraboloid in the y = 0 plane.
While most people probably think of “parabola” as an equation of the form z = ax2, you can rewrite it in the form x2 = 4pz, by picking the right p (specifically p = 1/(4a)). This form is helpful here, because p happens to be the distance from the parabola’s vertex to its focus. (Read about conic sections for why this is, perhaps in your calc 2 book.)
Having put the equation for the trace into the x2 = 4pz form, the example finishes by solving for p to find out where the focus must be.
Cylinders and Quadric Surfaces
Section 11.6
Cylinders
Key Ideas
Any curve can form a cylinder by “pushing” it along parallel lines
Examples
A new Mathematica function that’s helpful for working with those of these equations that are “explicit” equations for a surface, i.e., that give z as an explicit function of x and y: Plot3D. See this notebook for examples.
Is the surface defined by z = x2 + y a cylinder (similar to Example 11.6.1b)? Yes, because it’s a parabola pushed along rising lines parallel to the yz-plane:
How about the plane y = 2? Yes, it’s a straight line at y = 2 and perpendicular to the y axis, pushed along other lines parallel to the x or z axes.
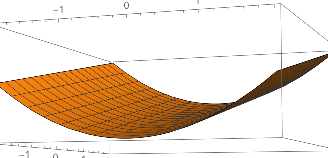
How about the surface z = x2 - y2? No, there’s no way to push a trace (or other cross-section) of this along straight parallel lines to produce the whole figure:

When we talk about lines in space, remind me to talk about how those ideas can be used to prove that something is a cylinder.
Quadric Surfaces
The last figure above, that’s not a cylinder, is a quadric surface: a hyperbolic paraboloid.
Key Ideas
The quadrics are produced by equations in 3 variables, involving second powers, first powers, and a constant.
They include lots of common shapes.
Next
Alternative coordinate systems for space: spherical and cylindrical coordinates.
Read section 11.7.