Questions?
Vectors in 3 (or More) Dimensions
“Working with Vectors in R3” in section 11.2.
Key Ideas
Vector operations:
- Vector addition and subtraction ( done componentwise)
- Scalar product
- Magnitude (length)
Component notation (⟨ x,y,z ⟩)and i, j, k (standard unit vector) notation
Prove things about vector operations by decomposing them into scalar operations.
Vectors, Velocity, and Speed
Suppose an airplane is moving with velocity 〈 4, 10, -2 〉meters/second relative to the surrounding air. That air is moving with velocity ⟨ 1, -1, 1 ⟩ meters/second relative to some fixed reference point.
Velocity = speed in a direction, speed = magnitude of velocity
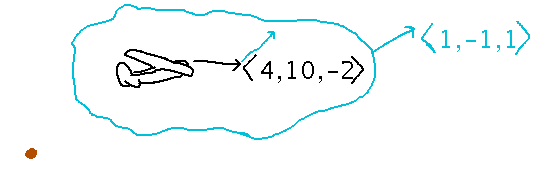
What is the plane’s velocity relative to the fixed reference?
Add the plane’s velocity relative to the air to the air’s velocity to get the total:
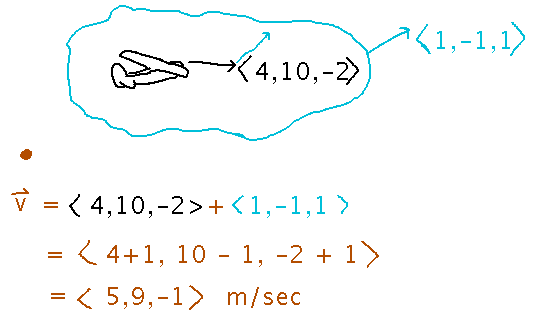
What is the airplane’s speed relative to the reference?
Since speed is the magnitude of velocity, use the magnitude formula:
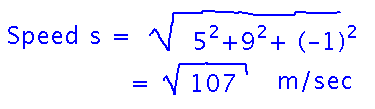
If the velocities all stay constant for 5 seconds, what is the plane’s displacement from its original position relative to the fixed reference?
Since velocity is in units of distance over time, multiply each component of the vector by the 5 seconds to get distance traveled. This is just scalar multiplication:
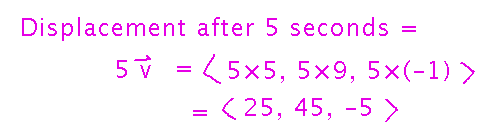
More than 3 Dimensions
For example, if some fast food chain with 5 restaurants has hamburger inventories in those restaurants of 70, 100, 65, 110, and 50 burgers, is that a vector?
It can be, with each “dimension” being a restaurant: ⟨ 70,100,65,110,50 ⟩. Vectors don’t have to be geometric or spatial things, and definitely don’t need to have only 2 or 3 dimensions.
Another good example is “feature vectors” in machine learning. By representing data on, say, what you buy online as a giant vector whose dimensions are individual items (men’s shoes, felt-tip markers, etc.) and whose values are the number of each item you have bought, all the mathematics of vectors can be brought to bear on the problems of identifying patterns in existing data and predicting them for the future.
Proofs about Vectors
The book claims that vector operations in 3 dimensions satisfy certain familiar algebraic properties (e.g., addition is commutative, scalar multiplication distributes over addition, etc.)
Prove one of these. For example prove that addition is commutative, u + v = v + u.
Start by expanding the vectors into components, the question is then whether ⟨ x,y,z ⟩ + ⟨ u,v,w ⟩ = ⟨ u,v,w ⟩ + ⟨ x,y,z ⟩, and you need to show that it does.
Start with one side of the equation, and apply definitions, other mathematical laws, etc. to rewrite it to the other side:
⟨ x,y,z ⟩ + ⟨ u,v,w ⟩ = ⟨ x+u, y+v, z+w ⟩ (definition of vector addition)
= ⟨ u+x, v+y, w+z ⟩ (commutativity of scalar addition)
= ⟨ u,v,w ⟩ + ⟨ x,y,z ⟩ (definition of vector addition, used in reverse)
The key thing here is the tactic of breaking vector addition down into multiple scalar additions, using what you know about algebra there, and then going back to vector form. This tactic works well for lots of proofs of vector properties.
Next
The dot product, a vector operation with a lot of uses in finding angles, lengths, projecting vectors onto each other, etc.
Read section 11.3.