SUNY Geneseo Department of Mathematics
Monday, April 30
Math 223 04
Spring 2018
Prof. Doug Baldwin
Available in “SampleFinal.pdf” file online, and through the “Review” module at the end of the course modules page.
Study day (Wednesday May 2), 11:30 - 12:30, in our regular classroom.
Tuesday, May 8, 12:00 noon to 3:20 PM, in our regular classroom.
Comprehensive, but with an emphasis on material since the 2nd hour exam (e.g., directional derivatives, gradients, Lagrange multipliers, multiple integrals & their applications, line integrals, vector fields, etc.)
Designed to be 2 to 2 1/2 times as long as the hour exams, but you have 4 times as much time.
Rules and format otherwise similar to hour exams, particularly including the open-references rule.
I’ll bring donuts and cider.
9 filled out as of this morning - thank you!
They are useful to me in improving courses for the future, and you get 1 printer dollar / SOFI. So please fill them out.
The vector field we looked at Wednesday, F(x,y) =〈 -y, x 〉had 0 flux around a closed curve. Is it source free?
Since F’s domain is the entire real plane, that domain is open and simply connected; therefore F is source free if it satisfies a component test:
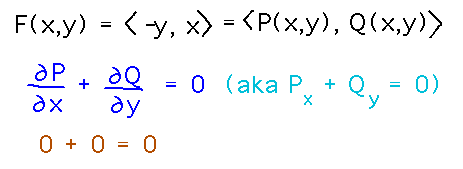
In this case both of the relevant partial derivatives are 0, so the component test is satisfied.
Source free fields have “stream functions” that play a similar role to potential functions in conservative fields, and can be found in a similar way (i.e., by realizing that the components of F are derivatives of the stream function and integrating -- see the textbook for details).
Source free vector fields as the equivalent for flux integrals of conservative fields for circulation.
Section 6.5.
Consider the vector field F(x,y,z) =〈 xy, yz, x2z 〉 = 〈 P, Q, R 〉
Find the divergence of F by simply plugging components into the formula:
Note that the “∇” notation for divergence and curl is mnemonic of the formulas for computing them:
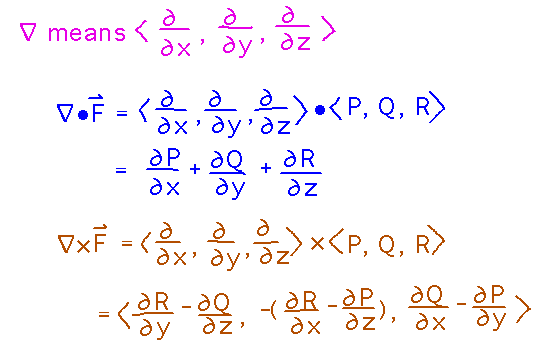
This is metaphorical rather than actual math, you can’t really “multiply” by differentiation operators, but the mnemonic works very well.
Notice that you’ve seen pieces of these operations before. In particular, a 2-dimensional divergence appears in the Green’s theorem double integral for flux, and the 3rd component of curl appears in the Green’s theorem double integral for circulation.
This isn’t coincidental, divergence does capture flux in the sense of whether a field diverges away from or converges towards a point, and curl captures circulation in the sense of a field’s tendency to represent a rotational force.
Both operators appear frequently in scientific fields that deal with vector fields, e.g., electro-magnetism, and so are worth knowing at least a little bit about.
Existence of divergence and curl, what they represent, and how to calculate them.