Review

Return to Course Outline

Previous Lecture

Things that you wanted to go over...

Bounds for Multiple Integrals

There’s no simple procedure for finding bounds.

The general idea is to identify some variable that lends itself well to being an independent variable from which to calculate bounds on the others, and then to figure out functions that calculate those bounds from the independent variable (and/or from previous “less dependent” ones).

Consider the book exercise of finding the volume in the first octant below the plane z = 10 - 2x - y. Solve this as a volume integral, i.e., an integral of 1 over the volume in question. The problem gives you an equation for z, so it makes a natural dependent variable.

Then we can more or less arbitrarily pick y as the independent variable, realizing that it can range from 0 to 10 while keeping z between 10 and 0 (i.e., in the first octant) and x ≥ 0 (also in the first octant).

Finally, we need bounds on x. The lower bound on x is 0 (keeping x in the 1st octant), while the upper bound is the line along which z = 0, i.e., solutions to 0 = 10 - 2x - y:

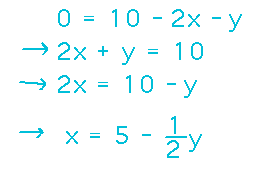
Now we can put these bounds together in integrals, ordered so that the integral with the independent variable is the outermost and the one with the most heavily dependent variable is innermost:

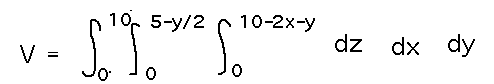
Planes, Lines, etc.

For example, a book exercise about whether planes are parallel, orthogonal, etc.

The key to deciding if planes are parallel is whether their normal vectors are parallel, i.e., whether one normal is simply a scalar multiple of the other. Normal vectors can, in turn, be read out from the coefficients of x, y, and z in a plane’s equation:

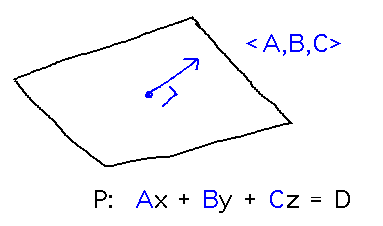
In the case of the book problem, the normals turn out to be parallel, so the planes are too:

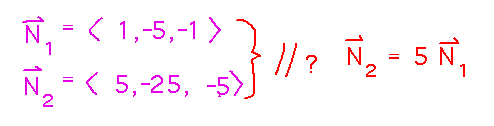
Key Point: Lots of the geometry of planes is in the normal vector.

Green’s Theorem

The P and Q functions that it constantly refers to are always the x and y components of the vector field function: F(x,y) = 〈 P(x,y), Q(x,y) 〉

Which derivative of P and Q you use, and in which order, depends on whether you are calculating a circulation integral (i.e., an integral of F dot tangent) or a flux integral (i.e., F dot normal).

Remembering the formulas is tricky; maybe associating them with divergence and curl and the dot product and cross product metaphors for those operations can help (or maybe not).

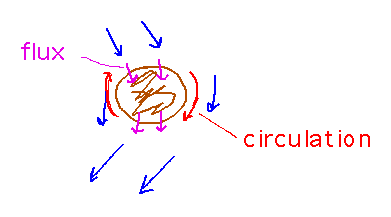
Circulation vs Flux

What is the physical significance of circulation vs flux?

Flux is the flow of a field across a boundary -- relatively easy to understand.

Circulation is the tendency of the vectors to make something spin around an axis perpendicular to the plane of the vectors, e.g., if the vectors were forces pushing harder on one side than on the other.

Parametric Curves

How to come up with parametric forms for a curve?

This is another place where there isn’t a simple algorithm you can use. Some ideas that might help are...

• Circles or circle-like figures usually involve sine and cosine
• If the curve is defined by an explicit equation y = f(x), let x = t and y = f(t), i.e., the parametric form can be r(t) = 〈 t, f(t) 〉
• If there’s some physical basis for the model, key physical quantities (e.g., time, angles, etc.) can be good parameters.

Example: find a parametric form for half an ellipse:

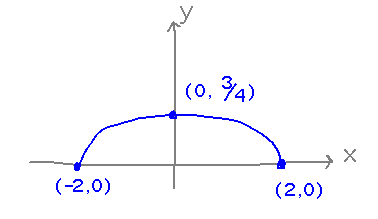
Starting building the parametric function from the function for a circle of radius a, r(t) = 〈 a cos t, a sin t 〉. But realize that an ellipse has different “radii” in each dimension, so find coefficients that will put the ellipse on the appropriate points at the necessary t values. It’s helpful here to think of t as geometrically being an angle, i.e., t = π/2 when the ellipse crosses the y axis, t = 0 and π when it reaches the x axis, etc. We can also use the idea that t is an angle to figure out the bounds on t for generating exactly half an ellipse.

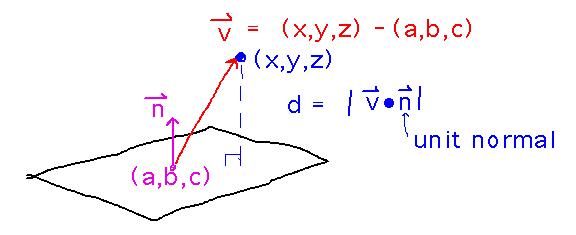
Distance from Point to Plane

Once again, the normal to the plane plays a crucial role.

In particular, the perpendicular distance from point (x,y,z) to the plane is the length of the projection onto the normal of a vector to (x,y,z) from any point (a,b,c) on the plane.

This projection is just the absolute value of the dot product of the vector to (x,y,z) and the unit normal:

(No Next Lecture)