SUNY Geneseo Department of Mathematics

Green’s Theorem, Part 3

Friday, April 27

Math 223 04
Spring 2018
Prof. Doug Baldwin

Return to Course Outline

Previous Lecture

Misc

Review Session

Study day (Wednesday May 2), 11:30 - 12:30, in our regular classroom.

Final Exam

Tuesday, May 8, 12:00 noon to 3:20 PM, in our regular classroom.

Comprehensive, but with an emphasis on material since the 2nd hour exam (e.g., directional derivatives, gradients, Lagrange multipliers, multiple integrals & their applications, line integrals, vector fields, etc.)

Designed to be 2 to 2 1/2 times as long as the hour exams, but you have 4 times as much time.

Rules and format otherwise similar to hour exams, particularly including the open-references rule.

I’ll provide a sample from a past semester.

I’ll bring donuts and cider.

SOFIs

6 filled out as of this morning - thank you!

They are useful to me in improving courses for the future, and you get 1 printer dollar / SOFI. So please fill them out.

Questions?

Green’s Theorem and Area

Find the area inside the curve r(t) = 〈 sin t cos t, 2 sin2t 〉, 0 ≤ t ≤ π.

A possibly helpful fact:

Antiderivative of sin squared x = x/2 - sin(2x)/4 + C

The key idea is that the double integral arising from Green’s theorem is an area if the integrand is 1. So Green’s theorem gives you a way to calculate area by evaluating a line integral around its boundary.

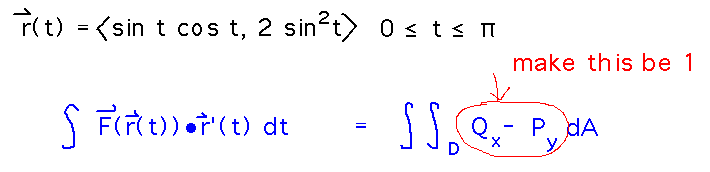
Circulation line integral equals double integral which equal area when integrand is 0

Since these area problems don’t involve any specific vector field, you can pick any one you like that makes the integrand 1. For example...

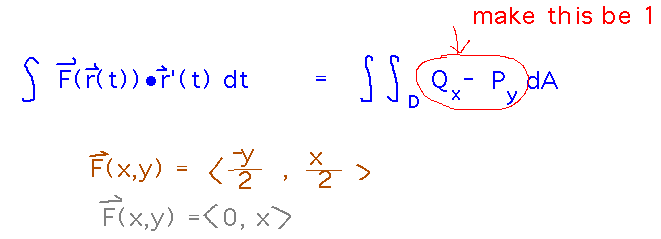
Vector fields ( -y/2, x/2 ) and ( 0, x ) both make Green integrand 0

(The first of these is the one usually described in textbooks.)

Choosing to use the second vector field (F(x,y) = 〈 0, x 〉), the area turns out to be...

Integrating path from 0 to pi yields pi/2

Key Point

Using Green’s theorem to calculate areas.

Source Free Fields

Source free fields are to flux integrals (integrals of F(r(t))•n(t)) as conservative fields are to circulation integrals (integrals of F(r(t))•r’(t)).

For example, for vector field F(x,y) =〈 P(x,y), Q(x,y) 〉

Source free fields have “stream functions” analogous to potential functions: Given source free field G(x,y) = 〈 P(x,y), Q(x,y) 〉, a function g(x,y) is a stream function for G if P = gy and Q = -gx.

Next

An example of a source free vector field (see the book’s discussion starting at the bottom of page 720).

Divergence and curl.

Read section 6.5.

Next Lecture