Gradient Fields

Return to Course Outline

Previous Lecture

Questions?

Circulation

Recall the beer brewing example from yesterday.

Using the same flow vector field, F(x,y) = 〈 y, -x 〉and keeping the bag of grains at the edge of the kettle, i.e., r(t) = 〈 sin t + 4, cos t 〉, find the circulation around the bag.

The field and parameteric curve (and the curve’s derivative and bounds) provide all the information we need to set up and evaluate the circulation integral:

Notice that this integral is exactly the same as the standard line integral of a vector field. Thus the various equivalent forms for that line integral that we discussed in the vector field line integrals class can all be used with circulation problems.

Circulation is harder to interpret physically than flux is. Rather than being an intuitive physical quantity, or even a measure of whether the vectors themselves describe circulating flows, the 2π we got for the circulation integral is an abstract measure of whether there’s an imbalance in the vectors’ lengths or directions that would (if they were forces) tend to make something placed in the field spin around itself.

Key Point

The circulation integral.

Gradient Vector Fields

Part of section 6.1.

The Idea

If f(x,y,z) is a function, its gradient is a vector field! f is called the “potential function” for the field.

Find the gradient field associated with f(x,y,z) = sin(xy) + cos(yz).

Start by finding the partial derivatives of f:

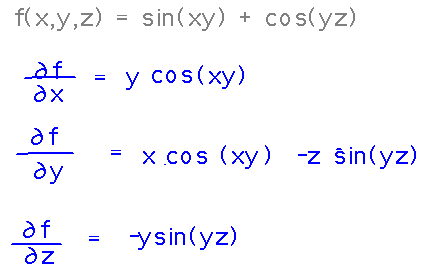
Then assemble them into a vector (the gradient of f), and there’s the vector field, i.e., a function that associates a vector with each point in space.

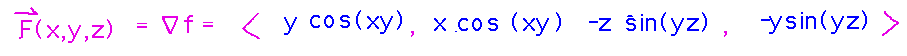
Challenge

If one exists, find a potential function for F(x,y) = 〈 2xy+y², x²+2xy 〉.

Idea: integrate the two components and see if both integrals come out the same. Or at least integrate one component and see what you get. You can tell which variable to integrate with respect to by which derivative of the potential function that component is.

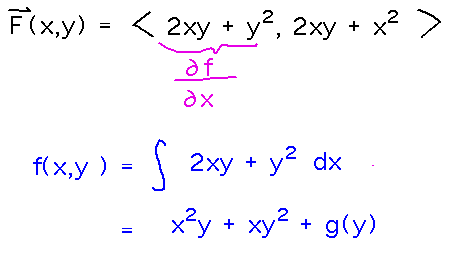
Notice that in indefinite multivariable integrals, the “constant” of integration is actually a function that can depend on all the variables except the one you’re integrating with respect to.

We’ll start taking this idea further next class, in the context of “conservative” fields (which happen to be gradient fields and vice versa).

Next

Conservative vector fields.

Read

• “Gradient Fields” in section 6.1 (if you haven’t already)
• “Curves and Regions” and “Fundamental Theorem for Line Integrals” in section 6.3.

Next Lecture