SUNY Geneseo Department of Mathematics

Line Integrals in Vector Fields, Part 1

Friday, April 13

Math 223 04
Spring 2018
Prof. Doug Baldwin

Questions?

Why are there different notations for vector field line integrals?

They start with the idea that the integral of a vector field over some curve is the integral of the component of the field that is tangent to the curve.

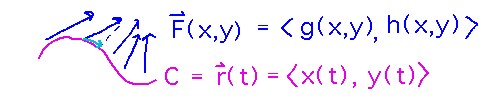
A path through some vectors, with one vector projected onto the tangent to the path

Since you can find the component of one vector parallel to another by taking the dot product of the first vector and a unit vector parallel to the second, this formulation of the line integral gives rise to its expression as

We already know how to express a line integral in terms of a parametric form of the curve, namely by expressing the function being integrated in terms of r(t) and multiplying by the magnitude of r’(t), so

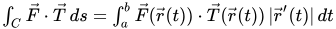
Integral of F dot T is integral of F(r(t)) dot T(r(t)) times magnitude of r(t)

Noticing that T, the unit tangent vector, is the derivative of r divided by the magnitude of that derivative derives the second common form of a vector field line integral:

Integral of F(r(t)) dot T(r(t)) times |r(t)| is integral of F(r(t)) dot r-prime(t)

Finally, if you think of r’(t) as being a vector containing the derivatives of x(t) and y(t), and expand the dot product into a sum, you get the third form (which is somewhat metaphorical, as it glosses over the parametric form of the curve and expressing the various functions and differentials in terms of that parametric form):

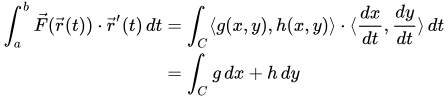
If F is the vector of g(x,y) and h(x,y), then integral of F(r(t)) dot r-prime(t) is integral of g dx plus h dy

Personally, I find the first of these forms most useful for understanding what a vector line integral is, the second most useful calculationally, and the third kind of a guideline/metaphor for how the components of the field function and parametric path interact.

Notice that if the vector field is a force, then the first form of the vector field line integral is also exactly the integral that gives you the work done by the force on a particle moving along the path. Thus vector line integrals are particularly useful in work calculations.

Line Integrals of Vector Fields

Part of section 6.2.

Example

Consider a space rock falling toward a star under the force of the star’s gravity, vector field G (which is conveniently expressed in ill-defined units that avoid needing any awkward constants in its formula; using real units would lead to similar equations but with uglier constants and larger values for the distances). the rock falls from position (2,2,2) to position (1,1,1).

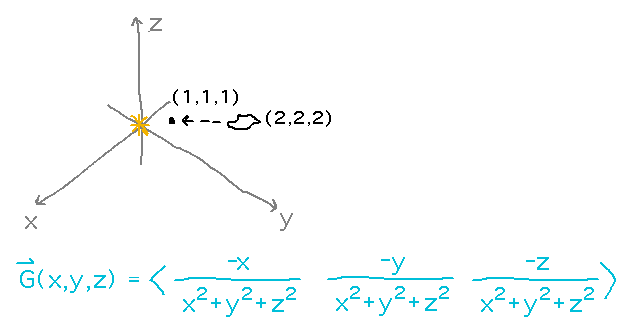
Star at origin of a coordinate system, rock moving from (2,2,2) to (1,1,1); G = ( -x/(x^2+y^2+z^2), -y/(x^2+y^2+z^2), -z/(x^2+y^2+z^2) )

What is the work done by gravity on this rock?

Start by finding a parametric function for the path the rock follows from (2,2,2) to (1,1,1). Since the path is a straight line, the most natural parametric form is probably r(t) = 〈 2-t, 2-t, 2-t 〉with 0 ≤ t ≤ 1. But you could also use r(t) = 〈 t, t, t 〉with t ranging from 2 down to 1, which is maybe less natural but makes the later integration simpler.

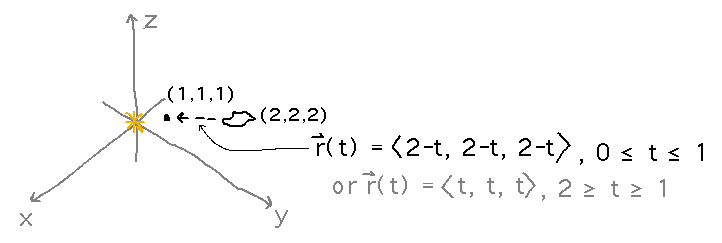
Star at origin with rock falling along path r(t) = (2-t,2-t,2-t) for t between 0 and 1 (or alternately, r(t) = (t,t,t) for t between 2 and 1)

Using the first of these parametric paths, the work, W, is simply the line integral of G along r (the first form of line integral notation in the question above), which can be evaluated using the second form of line integral notation:

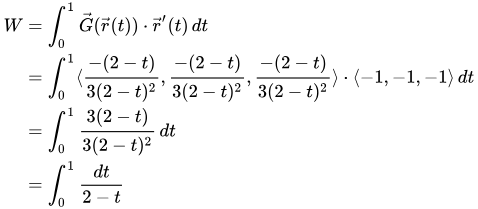
Work is integral of G(r(t)) dot r-prime(t) which is integral from 0 to 1 of dt over (2-t)

We can integrate this by making the substitution u = 2 - t, and so du = -dt, to get

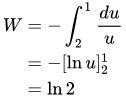
Work equals negative integral from 2 to 1 of du over u which equals ln(2)

So the star’s gravity gives the rock ln 2 units of additional energy as it falls.

More practice with line integrals of vector fields. No new reading.

Next Lecture