Conservative Vector Fields

Return to Course Outline

Previous Lecture

Questions?

Conservative Vector Fields

Section 6.3.

Motivation

Yesterday we saw that F(x,y,z) = 〈 y cos(xy), x cos(xy) - z sin(yz), -y sin(yz) 〉is a gradient vector field with potential function f(x,y,z) = sin(xy) + cos(yz).

Find the line integral of F along the path r(t) = 〈 π/2 e^t-1, t, e^t-1 - 1 〉for 0 ≤ t ≤ 1.

This is painful to solve the way we’ve been evaluating vector line integrals so far, but there’s a much easier way: use the Fundamental Theorem of Line Integrals!

This is only relevant when the vector field F has a potential function f (i.e., when F is the gradient of f), but in this case we do have a potential function, so we can use it.

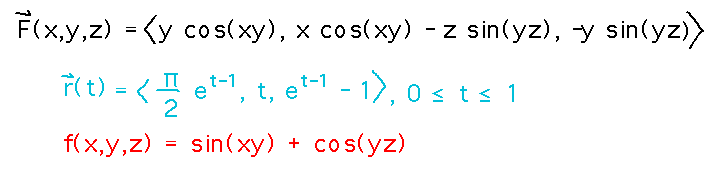
Start by finding r(1) and r(0):

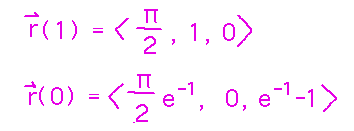
Then plug them into the potential function and evaluate:

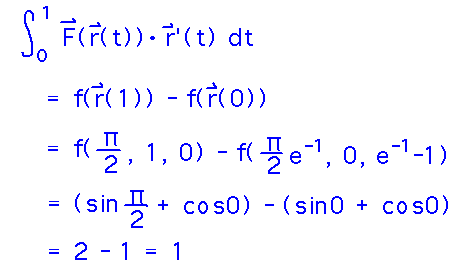
Consequences

Easy integration via the Fundamental Theorem isn’t the only consequence of a field being conservative. What are some others?

• Line integrals are path independent (i.e., the value of the integral only depends on the endpoints of the path, not what happens in between)
• Line integrals around closed curves are always 0 (because the starting point and ending point are equal).

The following statements are all equivalent to each other:

• F is a gradient field
• F is a conservative field
• F has a potential function
• F’s line integrals are (all) path independent
• (F passes the “cross partial” test, introduced in section 6.1 and to be discussed in class Monday)

So for what we know so far, finding a potential function for a vector field seems like a valuable thing to do, because doing it both tells us the field is conservative and gives us the tool we need for easy evaluation of line integrals.

Finding Potential Functions

Thursday’s Example

Finish the job we started Thursday of finding a potential function for F(x,y) = 〈 2xy + y², x² + 2xy 〉

Recall that you integrated 2xy + y² with respect to x to get x²y + xy² + h(y).

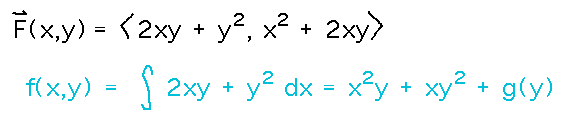
How can you find g(y)? One way (though not the standard textbook one) would be to now integrate x² + 2xy (the derivative with respect to y of the hypothetical potential function) with respect to y, and then try to reconcile the two results (both should be the same potential function). When we do this, we get

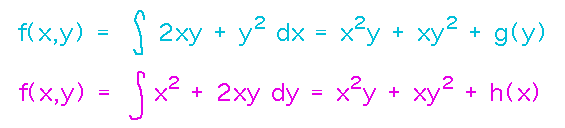
Since the two results are the same except for g(y) and h(x), we can conclude that g(y) and h(x) can represent constants, but not anything that involves y (which g(y) could introduce, but h(x) could never match) or x (for similar reasons). Thus we conclude that the potential functions for this field are all of the form f(x,y) = x²y + y²x + C where C can be any real number.

This approach feels a little vague when it comes to deciding what g(y) and/or h(x) would have to be in order to make the two integrals equal (up to a constant). There’s a slightly different approach that avoids this, which is presented in the text, and which we’ll pick up with Monday,

Key Points

The idea of conservative vector fields.

The idea of potential functions.

The fundamental theorem of line integrals.

There are easy ways to evaluate line integrals in conservative fields.

Next

Finish conservative vector fields, potential functions, etc.

Read “Conservative Vector Fields and Potential Functions” and “Testing a Vector Field” in section 6.3.

Next Lecture