SUNY Geneseo Department of Mathematics

Flux and Circulation

Wednesday, April 18

Math 223 04
Spring 2018
Prof. Doug Baldwin

Questions?

Flux Integral

Is the vector n appearing in the flux integral the principle unit normal vector?

In the initial definition of a flux integral, vector N (capital N) is a unit normal vector, but not necessarily the principle unit normal. Vector n (little n) appears in the calculationally simpler version, where it means a specific not-necessarily-unit normal vector based on the derivatives of the parametric path.

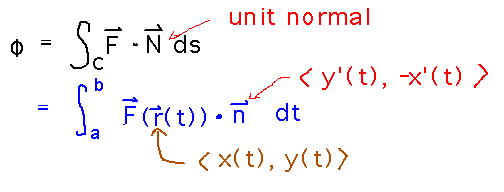
Vector N in integral of F dot N ds is a unit normal; vector n in integral of F(r(t)) dot n(t) is vector ( y'(t), -x'(t) )

Flux and Circulation

The last subsection of section 6.2.

Applications to Home Brewing

When I brew my own beer, one of the steps involves steeping a bag of grains in hot water. I circulate the bag around in a kettle, so that effectively the water is moving in a circle relative to the bag:

Vectors circulating through a small circle inside a larger circular region

This is, of course, an idealized model. In particular, it deals with 2 dimensional beer, i.e., we’re analyzing things in terms of a 2 dimensional vector field passing through a 2 dimensional circle, not a vector field in a 3 dimensional kettle passing through a spherical bag.

I want to get the most water flowing into the bag (and out again), i.e., the greatest flux of water through the bag.

What is this flux if the bag is at the edge of the kettle?

The first thing to do is find a parameterization of the bag, since it is the path you want to integrate along. Using a parametric form for a circle of radius 1, but adding 4 to the x component to move the circle to the edge of the kettle (which has radius 5) is a good way to come up with this parameterization.

Circular flow through circle r, r(t) = vector ( sin t + 4, cos t )

With r(t) defined, we can calculate all the parts that go into the flux integral, in particular F(r(t)) and n(t):

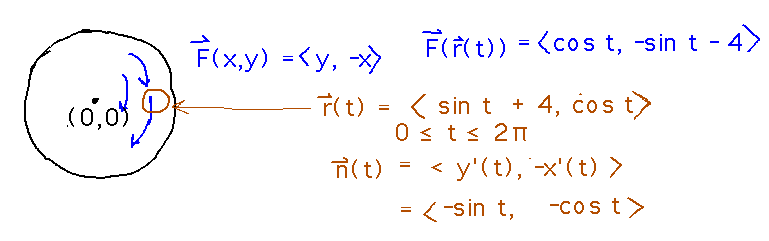
Circular flow F(r(t)) is vector ( cos t, -sin t - 4 ), flows through circle r = vector ( sin t + 4, cos t ); n is vector ( - sin t, -cos t);

Now we can put those pieces together into the flux integral and evaluate:

Flux is integral from 0 to 2pi of F(r(t)) dot n(t) which is -sin t cos t + sin t cos t + 4 sin t which integrates to 0

But how come this turned out to be 0? Intuitively we thought the greatest flux would be at the edge. The problem is that the flux integral calculates net flux, i.e., flux inward across a curve minus flux outward (or vice versa, depending on the orientation of the curve). In this case all the water that flows into the bag also flows out again.

What we really want to calculate for a better sense of how much water flows in (and out) is the flux across just the side of the bag that water flows in through. We can use the same parametric path to do that, just restricting the parameter to range over only the flow-ward half the bag:

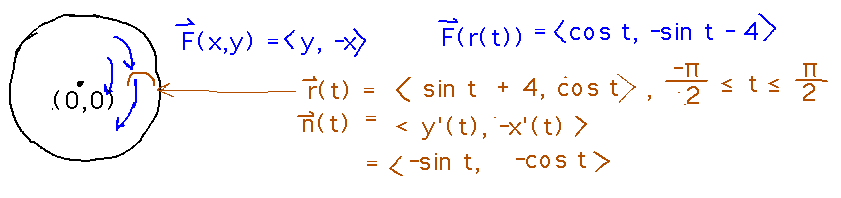
Circular flow through semicircle r(t) defined as vector ( sin t + 4, cos t ) for t between -pi/2 and pi/2

Now evaluating the new integral is just a matter of changing bounds; everything else we worked out before is still usable.

Integral of F(r(t)) dot n(t) from -pi/2 to pi/2 is 8

So, using inches and seconds as units of measurement, 8 square inches (remember this is 2 dimensional beer) of water flows into the bag per second.

Key Point

The flux integral and how to evaluate it.

A circulation integral example.

Start conservative vector fields.

Read

“Gradient Fields” in section 6.1.

Next Lecture