SUNY Geneseo Department of Mathematics

Integration in Polar Coordinates

Thursday, April 5

Math 223 04
Spring 2018
Prof. Doug Baldwin

Return to Course Outline

Previous Lecture

Misc

Correction to problem set 8, question 5.

Questions?

Double Integrals in Polar Coordinates

Section 5.3.

Motivation

Find the volume of the space between the surface z = √(x²+y²) and the disk inside x²+y²=1.

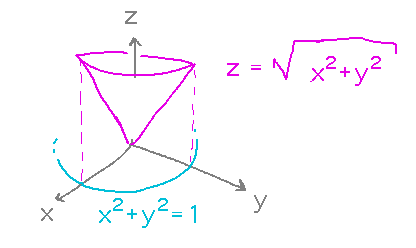
Upside down cone above a circle

There are several ways to do this. One that provides a nice test that calculus-based methods get it right is purely geometric, based on formulas for the volumes of cones and cylinders. This approach finds that the volume should be 2π/3.

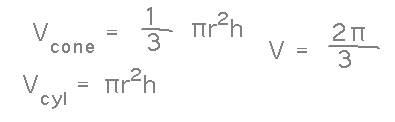
A cone's volume is 1/3 that of the enclosing cylinder, so volume outside the cone is 2 pi / 3

The obvious way to use recent calculus methods would be to integrate over the circular base in Cartesian coordinates, which quickly leads to a very difficult integral:

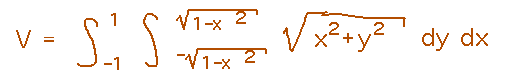
The integral of sqrt(x^2+y^2) is surprisingly hard to evaluate

But converting to polar coordinates makes the integration trivial:

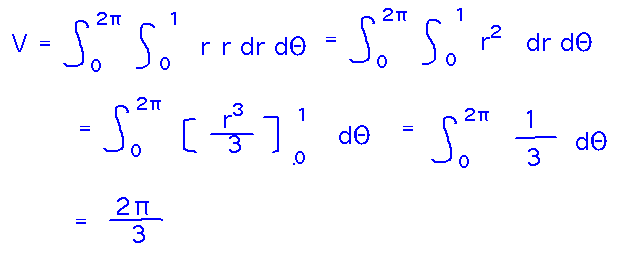
Integral in polar coordinates is from 0 to 2pi and 0 to 1 of r^2

Polar coordinates can simplify lots of volume integrations, especially when integrating over circles or parts of circles.

muPad

It’s interesting to look at what muPad does with the messy rectangular integral we found for the volume-under-cone problem. Working symbolically, it can’t really handle the integrals that arise.

muPad symbolic integration just yields another integral

But it can evaluate the integral numerically (using the numeric::int command)

More Practice

A building has a domed section defined by the surface z = √(4-(x²+y²)) with a walkway along the outer wall in the first quadrant. The bounds of the walkway are r = 1 and r = 2. What is the volume taken up by this walkway, assuming it extends all the way up to dome?

Quarter dome with section around outer rim marked

We can find this volume by integrating the height of the dome over the region covered by the walkway. This is much easier to do in polar coordinates than in Cartesian, since in polar coordinates the bounds of the walkway are just 1 ≤ r ≤ 2 and 0 ≤ Θ ≤ π/2.

Dome equation becomes sqrt(4-r^2), integrating over angles between 0 and pi/2 and radii between 1 and 2 yields pi/2 times sqrt(3)

Key Points

Integrating a function over a circle-like region is often simpler in polar coordinates than in rectangular.

How to convert a rectangular integral to polar.

Theory

Where does the extra factor of r come from in computing volumes as polar double integrals?

Volume integrals over polar regions are Riemann sums of volumes of thin columns. The volume of such a column is the area of its base times its height, but the bases are trapezoids, not rectangles. It turns out that the area of such trapedzoids is r dr dΘ. See section 5.3, subsection “Polar Rectangular Regions of Integration” for diagrams and more explanation.

Look at some applications of multiple integrals.

Read section 5.6.

Next Lecture