Applications of Multiple Integrals

Return to Course Outline

Previous Lecture

Questions?

Mass, Moment, Etc.

Section 5.6.

Example

“Indiana Jones and the Pyramid of Peril.” Indiana Jones has found the fabled Pyramid of Peril. A phenomenal treasure is tied to the Pyramid, and Indy can claim it if he cuts the rope leading to the treasure. But the Pyramid is unbalanced, and cutting the rope will cause it to topple over, releasing deadly snakes and otherwise causing mayhem. While the smart thing to do would be to flip the Pyramid over so it rests on a flat side, movie sales will be better if Indy delicately tilts the Pyramid so its center of mass is positioned exactly above its balance point and then cuts the rope.

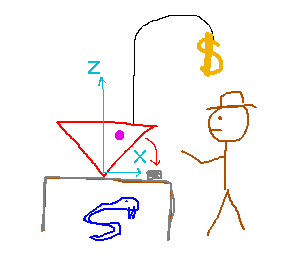
So there are two key questions for Indy:

• What is the mass of the pyramid?
• Where is its center of mass?

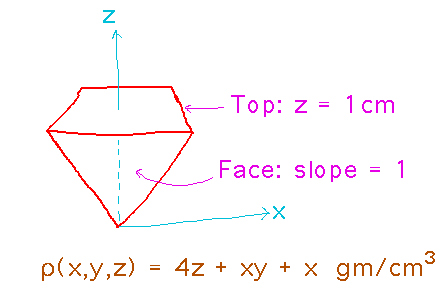
The Pyramid is balanced with its point at the origin. The Pyramid is 1 cm high, and its sides have slopes of 1 (or -1 on the negative sides of the x and y axes). The imbalance in the Pyramid is created by a non-uniform density ρ(x,y,z) = 4z + xy + x gm/cm³.

You can find the mass (which we’ll need for the center of mass anyhow) by integrating density over the Pyramid’s volume (based on the idea that mass equals density times volume).

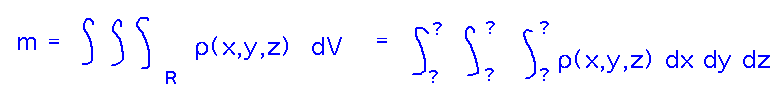
To find bounds for the integral, note that z ranges from 0 to 1, and determines the x and y extents of the Pyramid thanks to the z = ±x, z = ±y relations with the Pyramid’s sides. So integrate with z ranging from 0 to 1, and x and y ranging from -z to +z:

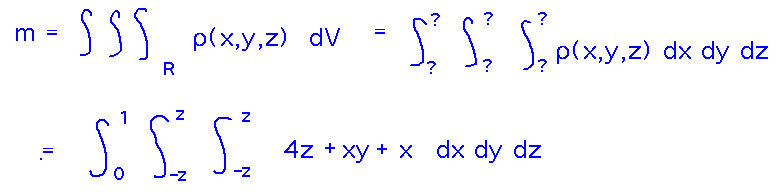
The rest of the integral is straightforward if tedious to evaluate:

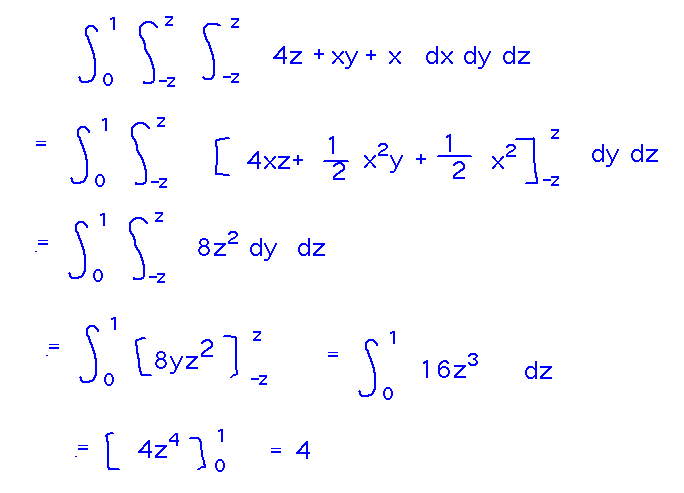
So the Pyramid’s mass is 4 grams.

Key Points

There are formulas for mass, center of mass, moment, etc.

The formulas are based on integrating density over volumes or areas.

Next

Finish finding the Pyramid of Peril’s center of mass.

Next Lecture