SUNY Geneseo Department of Mathematics
Wednesday, April 4
Math 223 04
Spring 2018
Prof. Doug Baldwin
Section 5.2.
Find the volume of that part of the cylinder of radius 1 centered on the z axis that lies between the z = 0, x ≥ 0 halfplane and the plane z = 2x.
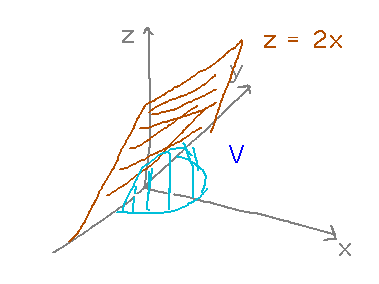
The first, and hardest, step is figuring out what the bounds of integration should be. The main choice is between treating x or y as the independent variable. It seems a little cleaner to use y, since it ranges from -1 to 1, and at each value in that interval x ranges from 0 out to the edge of the radius-1 semicircle. The integrand is just 2x -- think of this as a Riemann sum of the volumes of infinitely thin rectangles, then at each (x,y) point the height of the rectangle is just the distance to the z = 2x plane, i.e., 2x.
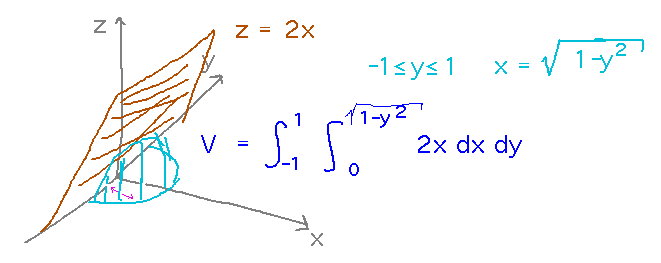
Once we make these decisions, evaluating the integral proceeds much like it has for other iterated integrals:
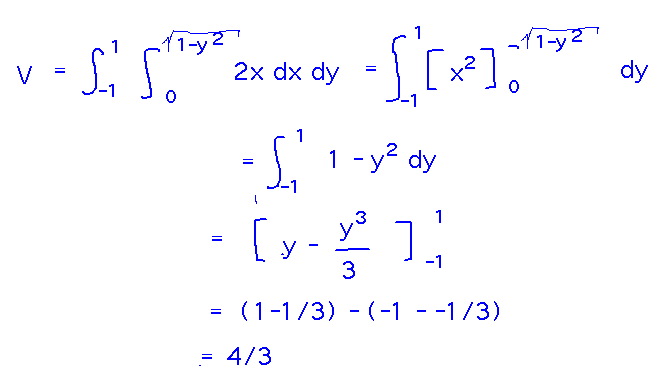
As a final remark, notice that you could also think of this as a triple integral, aka a Riemann sum of infinitely tiny cubes that fill the volume inside the wedge:
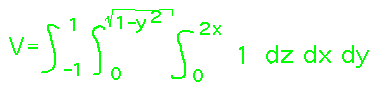
Calculationally this is less direct than what we did, since it requires evaluating a third integral whose effect will be to give us the integrand we started with. But this approach does illustrate how thinking in terms of multivariable functions gives you multiple ways to approach things like area and volume.
Let R be the region in the xy plane consisting of the rectangle with corners (-1,0), (1,0), (1,1), (-1,1) plus the area under the curve y = 2 - x2 but above that rectangle. Find the volume between the surface z = xy + 2y and above R.
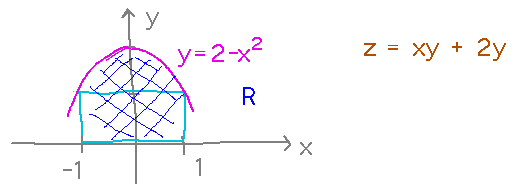
One way to think about this (admittedly the one the wording of the question encourages you to think of) is that it’s an integral over 2 regions, the rectangle and the parabola. Then you can use a theorem that says that a multiple integral over regions that don’t overlap except maybe at their boundaries is the sum of the integrals over each region.
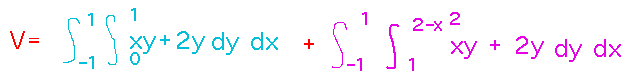
But you can also think of it as just the region between the x axis and the parabola, with x between -1 and 1.
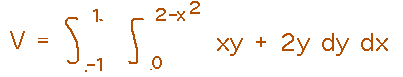
Either approach works, the main point is that there are many ways to think about the regions you’re integrating over.
Fnding bounds is typically the most important (and hardest) step in integrating over a nonrectangular region.
There are usually multiple plausible choices, some of which make integration easier than others.
Double integrals in polar coordinates.
Read section 5.3.