Integration over General Regions, Part 1

Misc

Problem set on extreme values and optimization (and a little bit on integrals).

Questions?

Integrals over General Regions

Section 5.2.

Example

Find the volume between z = cos(x+y) and the triangle with vertices (0,0), (π/2,0), (0,π/2) in the xy plane.

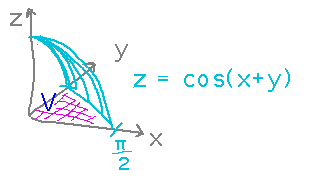
The first step is to decide what region to integrate over.

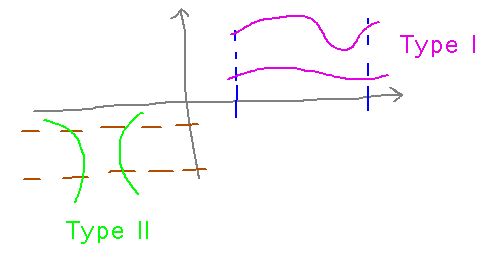
Question: what is the difference between type I and type II regions?

• Type I: it’s easiest to express y in terms of x.
• Type II: it’s easiest to to talk about x in terms of y.

The region for this problem is a right triangle with legs along the x and y axes, and hypotenuse along the line x + y = π/2. Rewriting this equation for the hypotenuse gives us a way to think of the region as a type I, i.e., bounded between x = 0 and x = π/2, with the y values for each x ranging from 0 to π/2 - x:

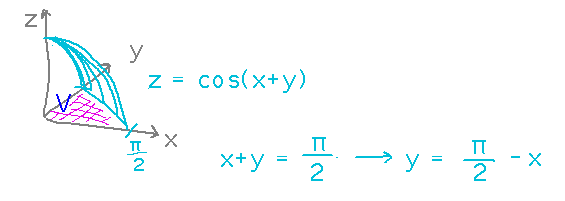
With these bounds in mind, we can set up the integral and start integrating.

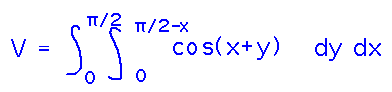
The first thing we run into is the need to integrate cos(x+y) with respect to y. Keeping in mind that for purposes of this integral we can pretend x is a constant, we can use a substitution to evaluate the integral:

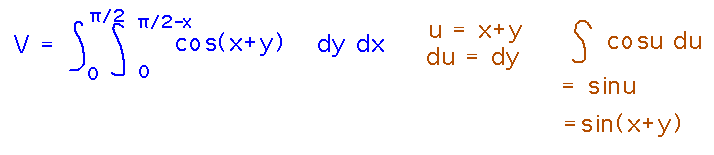
Finally, use the results of the substitution to finish the integration:

Nonrectangular Regions in muPad

We can double-check our result above against muPad.

You can use variables and expressions as bounds in the int command.

Key Points

Procedure for integrating over some nonrectangular regions:

1. Decide what variable(s) to treat as independent
2. Find functions to calculate the other variable(s) from the independent one(s)
3. Results from (1) and (2) become bounds on integrals and define order of integration (independent variables have be outside dependent ones)
4. Evaluate the integral, noting that bounds can be expressions instead of constants, and that you evaluate definite integrals with such bounds by substituting the expressions into the antiderivative just as if the bounds were constants.

Next

More practice integrating over nonrectangular regions.