Questions?
Integrals over Rectangular Regions
Section 5.1.
Example
Integrate z = x2 cosy over the region -1 ≤ x ≤ 1, 0 ≤ y ≤ π/2.
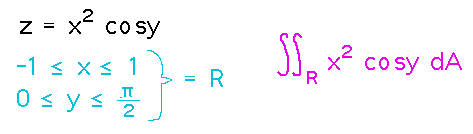
One way to approach this is to notice that it is an integral of the product of a function of x (x2) times a function of y (cos y), and so can be integrated as the product of the single-variable integrals of those functions:

This rule is handy, but is also simply a consequence of the general strategy for evaluating iterated integrals as a series of integrals in which all variables except the current variable of integration are temporarily treated as constants (in which case functions of other variables can be factored out of the current integral). So we could also evaluate this example as a series of nested integrals:
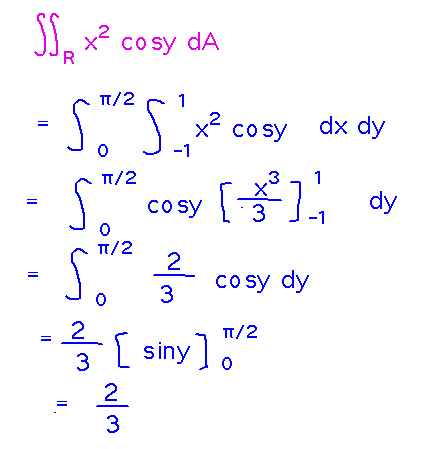
More Dimensions?
Can you integrate w = xy2 + x2z over 0 ≤ x ≤ 2, 0 ≤ y ≤ 1, 1 ≤ z ≤ 2?
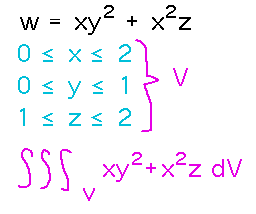
Sure, ideas for integrating functions with 2 variables generalize to functions of more variables.
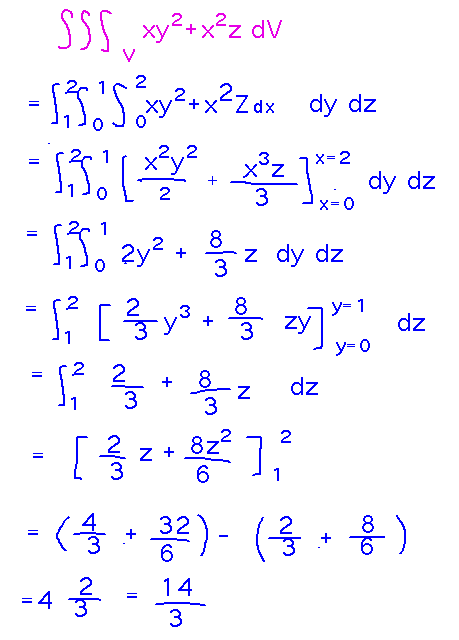
Another interesting observation: if you break this into the sum of 2 integrals (which is allowed by properties of multiple integrals), you get 2 integrals with just 2 variables apiece, and it seems they can be integrated as double integrals.
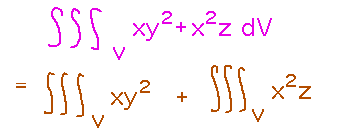
But unfortunately, this second claim isn’t really true: The 2 integrals you get from splitting are still integrals over 3 dimensions, and still have to be integrated over their “missing” dimensions (z in the first new integral, y in the second). In this particular problem the regions over which we’re integrating in z and y happen to be of size 1, so the effect of those integrations is to multiply by 1, i.e., no change to the final value. But if, for example, the regions were of some other size the answers you get by splitting the original 3 dimensional integral into 2 2 dimensional ones would be wrong.
Applications
What is the average value of z = x2 + y2 over the region 0 ≤ x ≤ 1, 0 ≤ y ≤ 2?
Find it by integrating over the region, and then dividing by the area of the region. This is geometrically exactly analogous to finding the average value of a single variable function by integrating over some interval and dividing by the length of the interval.
Integration in muPad
The int command evaluates an integral with respect to a single variable.
Use nested int commands to evaluate a multidimensional integral.

Key Points
Methods for evaluating multiple integrals.
The methods presented in this reading for 2 dimensions actually apply to any number of dimensions.
Evaluating multiple integrals in muPad.
Multiple integrals have applications, e.g., average values of multivariable functions.
Next
Integration over more general regions.
Read section 5.2.