Geneseo Math 223 04 Absolute Extrema and Optimization

Misc

New Things in Canvas

There’s now a set of sample exam questions with solutions available on Canvas.

There’s also a table showing how I converted numeric grades to letter grades last time I taught this course; the conversion won’t be exactly the same this semester, but historical information might give you some sense of how you’re doing.

Problem Set 7

On the chain rule for partial derivatives, directional derivatives, gradients.

See the handout for details.

Questions?

Finish Absolute Extreme Values

For z = x³/3 - x² + y² + 2y on -3 ≤ x ≤ 3, -2 ≤ y ≤ 2

Critical points:

(0, -1), z = -1
(2, -1), z = -7/3

Candidate extreme values on boundary:

(-3, -1, -19)
(3, -1, -1)
(0, -2, 0)
(2, -2, -4/3)
(0, 2, 8)
(2, 2, 20/3)

What more do we need? Values of z at the corners!

(3, 2, 8)
(-3, -2, -18)
(-3, 2, -10)
(3, -2, 0)

Now look for the minimum and maximum z values in all these points, and get...

Maximum = 8 at (0,2) and (3,2)
Minimum = -19 at (-3,-1)

Key Point

The process for finding absolute extremes; in particular remember to check boundaries and corners.

Lagrange Multipliers

Section 4.8.

A method for solving optimization problems with a constraint, i.e., problems in which you want to minimize or maximize something, but have to do it while preserving some relationship between the variables. In calculus 1 you may have seen some such problems, in particular ones where the constraint lets you express the problem as a single-variable one. Lagrange multipliers allow you to solve some optimization problems that can’t be turned into single-variable problems in this way.

Example

Find the points on the hyperbola x² - (y-1)² = 1 that are closest to the origin.

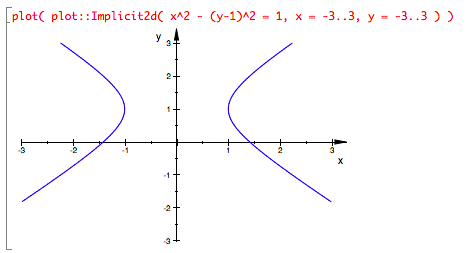
Horizontal hyperbolas slightly above the origin

While not described as such in the problem, there is a function here to minimize (i.e., an “objective function”), namely the distance from the origin to point (x,y), and a constraint on x and y.

x^2-(y-1)^2 = 1 is constraint, minimize R = x^2 + y^2

So we can use the method of Lagrange multipliers, as described in the reading, to solve this. (We could also use the constraint to deduce that x² = 1 + (y-1)² and solve it as a single-variable problem, but we’ll use it as an opportunity to look at Lagrange multipliers instead.) Work it out in class or at least before Wednesday’s class, and come with a solution or questions we need to discuss.

Key Points

Lagrange multipliers as a technique for solving optimization problems.

Finish Lagrange multipliers.

Review questions / requests for the exam.